题目内容
18.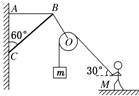 如图所示,轻质BC的C点用光滑铰链与墙壁固定,杆的B点通过水平细绳AB使杆与竖直墙壁保持60°的夹角.若在B点用细绳悬挂一个定滑轮(不计重力),某人用它匀速地提起重物.已知重物的质量m=30kg,人的质量M=50kg,连接人的绳子与水平方向的夹角始终保持30°,g取10m/s2.试求:(结果可以用根号表示)
如图所示,轻质BC的C点用光滑铰链与墙壁固定,杆的B点通过水平细绳AB使杆与竖直墙壁保持60°的夹角.若在B点用细绳悬挂一个定滑轮(不计重力),某人用它匀速地提起重物.已知重物的质量m=30kg,人的质量M=50kg,连接人的绳子与水平方向的夹角始终保持30°,g取10m/s2.试求:(结果可以用根号表示)(1)细绳BO上的张力大小;
(2)轻杆BC和细绳AB所受的力的大小.
分析 绳子对滑轮的压力的合力在两个分力的角平分线上,结合几何关系得到绳子对人的拉力与水平方向的夹角,然后对人受力分析,根据平衡条件并结合正交分解法列式求解;
解答 解:(1)对重物,由平衡条件知绳子拉力FT=mg=300 N
对定滑轮,如图所示,
FTBO=2FTcos 30°=300$\sqrt{3}$ N
(2)将B点的拉力FTOB分解,如图所示,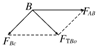
则细绳所受力为:FAB=$\frac{{F}_{TBO}}{sin30°}$=600$\sqrt{3}$ N
轻杆所受力为:FBC=$\frac{{F}_{TBO}}{tan30°}$=900 N.
答:(1)细绳BO上的张力大小为300$\sqrt{3}$ N;
(2)轻杆BC和细绳AB所受的力的大小分别为900 N和600$\sqrt{3}$ N.
点评 本题关键灵活地选择研究对象,然后对物体受力分析,根据平衡条件并结合分解法列式求解,不难.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
8.自行车在平直公路上匀速行驶,前后车轮所受地面摩擦力方向为( )
| A. | 前后车轮所受摩擦力都向后 | |
| B. | 前后车轮所受摩擦力都向前 | |
| C. | 前车轮所受摩擦力向后,后车轮所受摩擦力向前 | |
| D. | 前车轮所受摩擦力向前,后车轮所受摩擦力向后 |
9.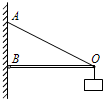 城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂.图是这类结构的一种简化模型,硬杆左端可绕通过B点且垂直于纸面的轴无摩擦的转动,右端O点通过钢索挂于A点,钢索和硬杆所受的重力均可忽略.有一质量不变的重物悬挂于O点,现将钢索缓慢变短,并使钢索的悬挂点A缓慢向下移动,以保证硬杆始终处于水平.则在上述变化过程中,下列说法中正确的是( )
城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂.图是这类结构的一种简化模型,硬杆左端可绕通过B点且垂直于纸面的轴无摩擦的转动,右端O点通过钢索挂于A点,钢索和硬杆所受的重力均可忽略.有一质量不变的重物悬挂于O点,现将钢索缓慢变短,并使钢索的悬挂点A缓慢向下移动,以保证硬杆始终处于水平.则在上述变化过程中,下列说法中正确的是( )
 城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂.图是这类结构的一种简化模型,硬杆左端可绕通过B点且垂直于纸面的轴无摩擦的转动,右端O点通过钢索挂于A点,钢索和硬杆所受的重力均可忽略.有一质量不变的重物悬挂于O点,现将钢索缓慢变短,并使钢索的悬挂点A缓慢向下移动,以保证硬杆始终处于水平.则在上述变化过程中,下列说法中正确的是( )
城市中的路灯、无轨电车的供电线路等,经常用三角形的结构悬挂.图是这类结构的一种简化模型,硬杆左端可绕通过B点且垂直于纸面的轴无摩擦的转动,右端O点通过钢索挂于A点,钢索和硬杆所受的重力均可忽略.有一质量不变的重物悬挂于O点,现将钢索缓慢变短,并使钢索的悬挂点A缓慢向下移动,以保证硬杆始终处于水平.则在上述变化过程中,下列说法中正确的是( )| A. | 硬杆对O点的弹力不变 | |
| B. | 钢索对O点的拉力变小 | |
| C. | 钢索和硬杆对O点的作用力的合力变大 | |
| D. | 钢索和硬杆对O点的作用力的合力不变 |
6.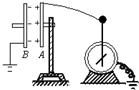 如图所示,用静电计可以测量已充电的平行板电容器两极之间的电势差,现使A板带正电,B板带负电,则下列说法正确的是( )
如图所示,用静电计可以测量已充电的平行板电容器两极之间的电势差,现使A板带正电,B板带负电,则下列说法正确的是( )
 如图所示,用静电计可以测量已充电的平行板电容器两极之间的电势差,现使A板带正电,B板带负电,则下列说法正确的是( )
如图所示,用静电计可以测量已充电的平行板电容器两极之间的电势差,现使A板带正电,B板带负电,则下列说法正确的是( )| A. | 将B板稍微向右移,静电计指针张角将变小 | |
| B. | 若将B板稍微向上移,静电计指针张角将变小 | |
| C. | 若将B板拿走,静电计指针张角变为零 | |
| D. | 若将玻璃板插入两极板之间,静电计指针张角将变小 |
19.在2008年北京奥运会上,牙买加选手博尔特是公认的世界飞人,在男子100m决赛和男子200m决赛中分别以9.69s和19.30s的成绩打破两项世界纪录,获得两枚金牌.关于他在这两次决赛中的运动情况,下列说法中不正确的是( )
| A. | 200m决赛的平均速率约为10.36m/s | |
| B. | 200m决赛的位移是100 m决赛的两倍 | |
| C. | 100m决赛的平均速度约为10.32m/s | |
| D. | 100m决赛的最大速度由题目数据无法求出 |
 如图所示,A为橡胶圆盘,其盘面竖直,B为紧贴A的毛皮,在靠近盘的边沿外的小磁针静止在图示位置,当沿图中箭头的方向转动把手C时,小磁针将发生什么现象?
如图所示,A为橡胶圆盘,其盘面竖直,B为紧贴A的毛皮,在靠近盘的边沿外的小磁针静止在图示位置,当沿图中箭头的方向转动把手C时,小磁针将发生什么现象?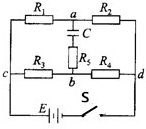 在如图所示的电路中,定值电阻R1=7Ω、R2=3Ω、R3=1Ω、R4=4Ω、R5=5Ω,电容器的电容C=2μF,电源的电动势为E=20V,忽略电源的内阻.若将开关S闭合,求:
在如图所示的电路中,定值电阻R1=7Ω、R2=3Ω、R3=1Ω、R4=4Ω、R5=5Ω,电容器的电容C=2μF,电源的电动势为E=20V,忽略电源的内阻.若将开关S闭合,求: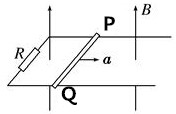 如图所示,一对光滑的平行金属导轨固定在同一水平面内,导轨的间距l=0.4m,在导轨的左端接有阻值R=0.2Ω的电阻,一质量m=0.1kg、电阻r=0.1Ω的金属棒PQ垂直于导轨放置其上,整个装置竖直向上、磁感应强度B=0.4T的匀强磁场中.现对金属棒施加一在水平向右的作用力,使其由静止开始以a=2m/s2的加速度做匀加速直线运动,在金属棒的位移x=9m时撤去外力,金属棒继续运动一段距离后停下来.已知导轨足够长且电阻不计,金属棒在运动过程中始终与导轨保持良好接触.撤去外力后,求:
如图所示,一对光滑的平行金属导轨固定在同一水平面内,导轨的间距l=0.4m,在导轨的左端接有阻值R=0.2Ω的电阻,一质量m=0.1kg、电阻r=0.1Ω的金属棒PQ垂直于导轨放置其上,整个装置竖直向上、磁感应强度B=0.4T的匀强磁场中.现对金属棒施加一在水平向右的作用力,使其由静止开始以a=2m/s2的加速度做匀加速直线运动,在金属棒的位移x=9m时撤去外力,金属棒继续运动一段距离后停下来.已知导轨足够长且电阻不计,金属棒在运动过程中始终与导轨保持良好接触.撤去外力后,求: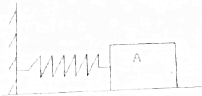 水平桌面上木块质量为15千克,与桌面之间的最大静摩擦力为为60牛.弹簧的劲度系数k=5000牛/米,如图所示,在木块A上施加向左的水平推力,当弹簧被外力压缩1厘米时,撤去外力后,物体将处于静止状态,此时木块受到的摩擦力为50牛,当压缩量大于1.2厘米时,撤去外力后,木块将不能保持静止状态.
水平桌面上木块质量为15千克,与桌面之间的最大静摩擦力为为60牛.弹簧的劲度系数k=5000牛/米,如图所示,在木块A上施加向左的水平推力,当弹簧被外力压缩1厘米时,撤去外力后,物体将处于静止状态,此时木块受到的摩擦力为50牛,当压缩量大于1.2厘米时,撤去外力后,木块将不能保持静止状态.