题目内容
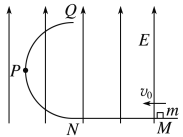
【题目】如图所示,在E=103 V/m的竖直匀强电场中,有一光滑半圆形绝缘轨道QPN与一水平绝缘轨道MN在N点平滑相接,半圆形轨道平面与电场线平行,其半径R=40 cm,N为半圆形轨道最低点,P为QN圆弧的中点,一带负电q=10-4 C的小滑块质量m=10 g,与水平轨道间的动摩擦因数μ=0.15,位于N点右侧1.5 m的M处,g取10 m/s2,求:
(1)小滑块从M点到Q点电场力做的功
(2)要使小滑块恰能运动到半圆形轨道的最高点Q,则小滑块应以多大的初速度v0向左运动?
(3)这样运动的小滑块通过P点时对轨道的压力是多大?
【答案】(1) - 0.08J(2) 7 m/s(3)0.6 N
【解析】
(1)W=-qE·2R W= - 0.08J
(2)设小滑块到达Q点时速度为v,
由牛顿第二定律得mg+qE=m![]()
小滑块从开始运动至到达Q点过程中,由动能定理得
-mg·2R-qE·2R-μ(mg+qE)x=![]() mv2-
mv2-![]() mv
mv![]()
联立方程组,解得:v0=7m/s.
(3)设小滑块到达P点时速度为v′,则从开始运动至到达P点过程中,由动能定理得
-(mg+qE)R-μ(qE+mg)x=![]() mv′2-
mv′2-![]() mv
mv![]()
又在P点时,由牛顿第二定律得FN=m ![]()
代入数据,解得:FN=0.6N
由牛顿第三定律得,小滑块通过P点时对轨道的压力FN′=FN=0.6N.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目