题目内容
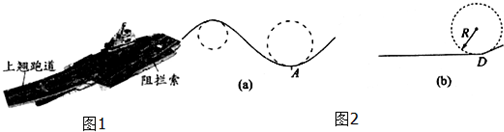
5. 如图所示是离心轨道演示仪结构示意图,光滑弧形轨道下端与半径为R的光滑圆弧轨道相连,整个轨道位于竖直平面内.质量为m的小球从弧形轨道上的A点由静止滑下,进入圆弧轨道后沿圆轨道运动,最后离开圆轨道,小球运动的圆轨道的最高点时,对轨道的压力恰好与它所受到的重力大小相等,重力加速度为g,不计空气阻力.求:
如图所示是离心轨道演示仪结构示意图,光滑弧形轨道下端与半径为R的光滑圆弧轨道相连,整个轨道位于竖直平面内.质量为m的小球从弧形轨道上的A点由静止滑下,进入圆弧轨道后沿圆轨道运动,最后离开圆轨道,小球运动的圆轨道的最高点时,对轨道的压力恰好与它所受到的重力大小相等,重力加速度为g,不计空气阻力.求:(1)小球运动到圆轨道的最高点时速度的大小;
(2)小球开始下滑的初始位置A点距水平面的竖直高度h.
分析 (1)小球做圆周运动,应用牛顿第二定律可以求出小球的速度.
(2)应用动能定理可以求出A点的高度.
解答 解:(1)小球做圆周运动,在圆轨道的最高点,由牛顿第二定律得:
N+mg=m$\frac{{v}^{2}}{R}$,
且N=mg
解得:v=$\sqrt{2gR}$;
(2)小球从A运动到圆轨道最高点过程中,由动能定理得:
mg(h-2R)=$\frac{1}{2}$mv2-0,
解得:h=3R;
答:(1)小球运动到圆轨道的最高点时速度的大小为$\sqrt{2gR}$;
(2)小球开始下滑的初始位置A点距水平面的竖直高度h为3R.
点评 本题考查了求小球的速度、释放点的高度,分析清楚运动过程,应用牛顿第二定律与动能定理可以正确解题.

练习册系列答案
相关题目
15.为测量电流表A的内阻(量程为50mA,内阻约10Ω),提供的实验器材有:
A.直流电压表V(0~3V,内阻约6KΩ)
B.定值电阻R1(5.0Ω~1A)
C.定值电阻R2(50.0Ω~0.1A)
D.滑动变阻器R(0~5Ω2A)
E.直流电源E(3V,内阻很小)
F.导线、电键若干

(1)实验中定值电阻R0应选用R2(选填“R1”或“R2”);
(2)在图1中虚线框内将实验电路原理图画完整;
(3)某同学在实验中测出7组对应的数据(见表):
请在图2所示坐标系中描点作出U-I图线.由图象可知,表中第3次实验数据有错误,此电流表的电阻为10Ω.(计算结果保留两位有效数字)
A.直流电压表V(0~3V,内阻约6KΩ)
B.定值电阻R1(5.0Ω~1A)
C.定值电阻R2(50.0Ω~0.1A)
D.滑动变阻器R(0~5Ω2A)
E.直流电源E(3V,内阻很小)
F.导线、电键若干

(1)实验中定值电阻R0应选用R2(选填“R1”或“R2”);
(2)在图1中虚线框内将实验电路原理图画完整;
(3)某同学在实验中测出7组对应的数据(见表):
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| U/V | 0.80 | 1.18 | 1.68 | 1.78 | 1.98 | 2.36 | 2.70 |
| I/mA | 14.0 | 20.0 | 24.0 | 30.0 | 24.0 | 40.0 | 46.0 |
16.在光滑的水平面上,质量为2kg的甲球以速度v0与乙球发生正碰,碰撞后,乙球的动量减少了6kg•m/s,则碰后甲球的速度为( )
| A. | v0-3 | B. | 3+v0 | C. | v0-12 | D. | 12+v0 |
12.图甲为一列简谐横波在t=0.10s时刻的波形图,P是平衡位置为x=1.0m处的质点,Q是平衡位置为x=4.0m处的质点,图乙为质点Q的振动图象,则( )
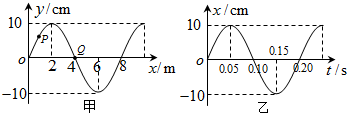
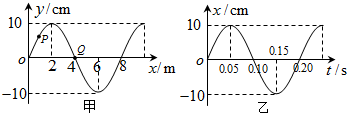
| A. | t=0.15s时,质点Q的加速度达到正向最大 | |
| B. | 质点Q简谐运动的表达式为x=10sin$\frac{π}{2}$t(cm) | |
| C. | 从t=0.10s到t=0.25s,质点P通过的路程为30cm | |
| D. | 从t=0.10s到t=0.25s,该波沿x轴负方向传播了6m |

 如图所示,一轻质弹簧一端固定,原来弹簧静止在光滑水平面上的无形变固体,在大小为F的水平恒力作用下由静止开始沿光滑水平面向右运动.在O点与弹簧接触后继续向前到B点时将外力f撤去,此时物体的速度为v,已知:AO=4s,OB=s,则撤去外力后物体的最大速度为$\sqrt{10Fs}$.
如图所示,一轻质弹簧一端固定,原来弹簧静止在光滑水平面上的无形变固体,在大小为F的水平恒力作用下由静止开始沿光滑水平面向右运动.在O点与弹簧接触后继续向前到B点时将外力f撤去,此时物体的速度为v,已知:AO=4s,OB=s,则撤去外力后物体的最大速度为$\sqrt{10Fs}$. 如图所示,一辆上表面光滑的平板车长L=4m,平板车上表面离地面高度为h=1.25m,平板车上后端有一挡板,紧靠挡板处有一可看成质点的小球,开始时小球与平板车一起向前做匀速运动,速度大小为v0=4.5m/s.某时刻小车开始刹车,加速度a=2.0m/s2.经过一段时间,小球从平板车前端滑落并落到水平地面上,设小球离家平板车对加速度没有影响.求:
如图所示,一辆上表面光滑的平板车长L=4m,平板车上表面离地面高度为h=1.25m,平板车上后端有一挡板,紧靠挡板处有一可看成质点的小球,开始时小球与平板车一起向前做匀速运动,速度大小为v0=4.5m/s.某时刻小车开始刹车,加速度a=2.0m/s2.经过一段时间,小球从平板车前端滑落并落到水平地面上,设小球离家平板车对加速度没有影响.求: