题目内容
 (2013?河池模拟)如图甲所示,一竖直平面内的轨道由粗糙斜面AD和光滑圆轨道DCE组成,AD与DCE相切于D点,C为圆轨道的最低点,将一小物块置于轨道ADC上离地面高为H处由静止释放,用力传感器测出其经过C点时对轨道的压力N,改变H的大小,
(2013?河池模拟)如图甲所示,一竖直平面内的轨道由粗糙斜面AD和光滑圆轨道DCE组成,AD与DCE相切于D点,C为圆轨道的最低点,将一小物块置于轨道ADC上离地面高为H处由静止释放,用力传感器测出其经过C点时对轨道的压力N,改变H的大小,可测出相应的N的大小,N随H的变化关系如图乙折线PQI所示(PQ与QI两直线相连接于Q点),QI反向延长交纵轴于F点(0,5.8N),重力加速度g取10m/s2,求:
(1)求出小物块的质量m;圆轨道的半径R、轨道DC所对应的圆心角θ;
(2)小物块与斜面AD间的动摩擦因数μ.
(3)若要使小物块能运动到圆轨道的最高点E,则小物块应从离地面高为H处由静止释放,H为多少?
分析:(1)从图象得到H=0时的弹力,即为物体的重力,从而得到物体的质量m;
(2)结合图象可以得到当H=0.2m时,物体恰好在斜面最低点,根据机械能守恒定律和向心力公式联立列式求解出圆轨道的半径R,然后可根据几何关系得到轨道DC所对圆心角;
(3)对滑块从最高点到C点的过程运用动能定理列式,再对最低点运用向心力公式和牛顿第二定律列式,联立后求解出弹力的一般表达式,再根据图象求解出动摩擦因素.
(2)结合图象可以得到当H=0.2m时,物体恰好在斜面最低点,根据机械能守恒定律和向心力公式联立列式求解出圆轨道的半径R,然后可根据几何关系得到轨道DC所对圆心角;
(3)对滑块从最高点到C点的过程运用动能定理列式,再对最低点运用向心力公式和牛顿第二定律列式,联立后求解出弹力的一般表达式,再根据图象求解出动摩擦因素.
解答:解:(1)如果物块只在圆轨道上运动,则由动能定理得mgH=
mv2解得v=
;
由向心力公式FN-mg=m
,得FN=m
+mg=
H+mg;
结合PQ曲线可知mg=5得m=0.5 kg.
由图象可知
=10得R=1 m.显然当H=0.2 m对应图中的D点,
所以cos θ=
=0.8,θ=37°.
(2)如果物块由斜面上滑下,由动能定理得:mgH-μmgcos θ
=
mv2
解得mv2=2mgH-
μmg(H-0.2)
由向心力公式得FN=m
+mg=
H+
μmg+mg
由向心力公式FN-mg=m
得FN=m
+mg=
μmg,R)H+
μmg+mg
结合QI曲线知
μmg+mg=5.8,解得μ=0.3.
(3)如果物块由斜面上滑下到最高点速度为v,
由动能定理得:mg(H-2R)-μmgcos θ
=
mv2 (1)
设物块恰能到达最高点:由向心力公式:mg=m
(2)
由(1)(2)式可得:H=15.1m
答:(1)求出小物块的质量m;圆轨道的半径R、轨道DC所对应的圆心角θ=37°;
(2)小物块与斜面AD间的动摩擦因数为0.3.
(3)若要使小物块能运动到圆轨道的最高点E,则小物块应从离地面高为15.1m处由静止释放.
| 1 |
| 2 |
| 2gH |
由向心力公式FN-mg=m
| v2 |
| R |
| v2 |
| R |
| 2mg |
| R |
结合PQ曲线可知mg=5得m=0.5 kg.
由图象可知
| 2mg |
| R |
所以cos θ=
| 1-0.2 |
| 1 |
(2)如果物块由斜面上滑下,由动能定理得:mgH-μmgcos θ
| (H-0.2) |
| sinθ |
| 1 |
| 2 |
解得mv2=2mgH-
| 8 |
| 3 |
由向心力公式得FN=m
| V2 |
| R |
2mg-
| ||
| R |
| 1.6 |
| 3 |
由向心力公式FN-mg=m
| v2 |
| R |
| v2 |
| R |
| 2mg-\f(8 |
| 3 |
| 1.6 |
| 3 |
结合QI曲线知
| 1.6 |
| 3 |
(3)如果物块由斜面上滑下到最高点速度为v,
由动能定理得:mg(H-2R)-μmgcos θ
| (H-0.2) |
| sinθ |
| 1 |
| 2 |
设物块恰能到达最高点:由向心力公式:mg=m
| v2 |
| R |
由(1)(2)式可得:H=15.1m
答:(1)求出小物块的质量m;圆轨道的半径R、轨道DC所对应的圆心角θ=37°;
(2)小物块与斜面AD间的动摩擦因数为0.3.
(3)若要使小物块能运动到圆轨道的最高点E,则小物块应从离地面高为15.1m处由静止释放.
点评:本题关键是对分析清楚滑块的各个运动过程,然后运用动能定理、机械能守恒定律和向心力公式,结合图象联立方程组求解.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
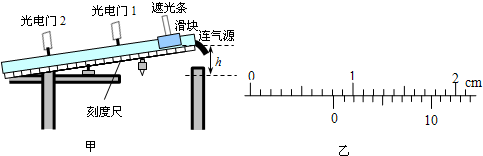
 (2013?河池模拟)中央电视台近期推出了一个游戏节目--推矿泉水瓶.选手们从起点开始用力推瓶一段时间后,放手让瓶向前滑动,若瓶最后停在桌上有效区域内,视为成功;若瓶最后不停在有效区域内或在滑行过程中倒下均视为失败.其简化模型如图所示,AC是长度为L1=5m的水平桌面,选手们可将瓶子放在A点,从A点开始用一恒定不变的水平推力推瓶,BC为有效区域.已知BC长度为L2=1m,瓶子质量为m=0.5kg,瓶子与桌面间的动摩擦因数μ=0.4.某选手作用在瓶子上的水平推力F=20N,瓶子沿AC做直线运动,(g取10m/s2)假设瓶子可视为质点,那么该选手要想游戏获得成功,试问:
(2013?河池模拟)中央电视台近期推出了一个游戏节目--推矿泉水瓶.选手们从起点开始用力推瓶一段时间后,放手让瓶向前滑动,若瓶最后停在桌上有效区域内,视为成功;若瓶最后不停在有效区域内或在滑行过程中倒下均视为失败.其简化模型如图所示,AC是长度为L1=5m的水平桌面,选手们可将瓶子放在A点,从A点开始用一恒定不变的水平推力推瓶,BC为有效区域.已知BC长度为L2=1m,瓶子质量为m=0.5kg,瓶子与桌面间的动摩擦因数μ=0.4.某选手作用在瓶子上的水平推力F=20N,瓶子沿AC做直线运动,(g取10m/s2)假设瓶子可视为质点,那么该选手要想游戏获得成功,试问: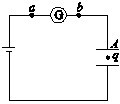 (2013?河池模拟)如图所示,用电池对电容器充电,电路a、b之间接有一灵敏电流表,两极板间有一个电荷q处于静止状态.现将两极板的间距变大,则( )
(2013?河池模拟)如图所示,用电池对电容器充电,电路a、b之间接有一灵敏电流表,两极板间有一个电荷q处于静止状态.现将两极板的间距变大,则( )