题目内容
【题目】一轻质细绳一端系一质量为m=0.05kg的小球A，另一端挂在光滑水平轴O上，O到小球的距离为L=0．lm，小球跟水平面接触，但无相互作用，在球的两侧等距离处分别固定一个光滑的斜面和一个挡板，如图所示，斜面与挡板间的水平距离s=2m，与滑块B间的动摩擦因数为μ=0.25．已知滑块B的质量也为m=0.05kg，现让B从斜面上高度h=5m处滑下，与小球发生弹性正碰，与挡板碰撞时不损失机械能．若不计空气阻力，并将滑块和小球都视为质点，（g取10m/s2），试问：
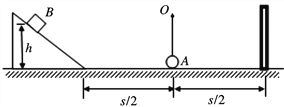
（1）求滑块B与小球第一次碰前的速度；（结果用根号表示）
（2）求滑块B与小球第一次碰后瞬间绳子对小球的拉力；
（3）滑块B与小球碰撞后，小球在竖直平面内做圆周运动，求小球做完整圆周运动的次数。
【答案】（1）
（2）48N（3）10次．
【解析】（1）滑块将要与小球发生碰撞时速度为v1，碰撞后速度为
，小球速度为v2．
根据能量守恒定律，得
解得
（2）A、B发生弹性碰撞，由动量守恒，得到： 
由能量守恒定律，得到： 
解得： 
即滑块B与小球第一次碰前的速度为
，碰后的速度为0．
碰后瞬间，有
解得 T=48N
即滑块B与小球第一次碰后瞬间绳子对小球的拉力48N．
（3）小球刚能完成一次完整的圆周运动，它到最高点的速度为v3，则有
小球从最低点到最高点的过程机械能守恒，设小球在最低点速度为v，根据机械能守
恒有
解得
滑块和小球最后一次碰撞时速度至少为
，滑块通过的路程为S′．
根据能量守恒有
解得s′=19m
小球做完整圆周圆周运动的次数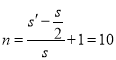
次
即小球做完整圆周运动的次数为10次．
练习册系列答案
相关题目
