题目内容
如图所示,在竖直平面内有一个半径为R的圆弧轨道。半径OA水平、OB竖直,一个质量为m的小球自A正上方P点由静止开始自由下落,小球沿轨道到达最高点B时恰好对轨道没有压力,已知PA=2R,重力加速度为g,则小球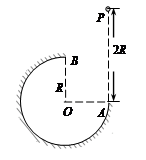
| A.从B点飞出后恰能落到A点 |
| B.从P到B的运动过程中机械能守恒 |
C.从P到B的运动过程中合外力做功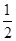 mgR mgR |
| D.从P到B的运动过程中克服摩擦力做功mgR |
C
解析试题分析:由“小球沿轨道到达最高点B时恰好对轨道没有压力”可知在B点时小球速度为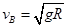 ,小球从B点飞出后
,小球从B点飞出后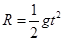 得
得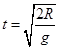 ,则水平距离
,则水平距离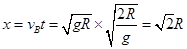 ,A错;若整个过程机械能守恒,从P点释放,到B点的速度应该是
,A错;若整个过程机械能守恒,从P点释放,到B点的速度应该是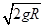 ,可见机械能减小,B错。从P到B的运动过程中,合外力做功等于物体动能的变化,即
,可见机械能减小,B错。从P到B的运动过程中,合外力做功等于物体动能的变化,即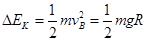 ,C正确。克服摩擦力做功等于系统能量的减少量
,C正确。克服摩擦力做功等于系统能量的减少量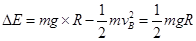 ,D错。
,D错。
考点:本题考查了圆周运动、平抛运动与能量守恒定律

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案如图所示,在竖直放置的半圆形容器的中心O点分别以水平初速度v1、v2抛出两个小球(可视为质点),最终它们分别落在圆弧上的A点和B点,已知OA与OB互相垂直,且OA与竖直方向成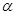 =37°角;则两小球初速度之比 ( )(sin37°=0.6,cos37°=0.8)
=37°角;则两小球初速度之比 ( )(sin37°=0.6,cos37°=0.8)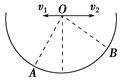
| A.0.6 | B.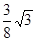 | C.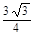 | D.0.8 |
如图所示,从地面上方不同高度处以水平速度va、vb抛出两小球a、b,结果a落在b初始位置的正下方,而b落在a初始位置的正下方,bc为过小球b初始位置的水平线,不计空气阻力,下列判断正确的有( )
| A.两球抛出时的初速度va<vb |
| B.若它们同时落地(不考虑它们在空中相碰弹射,可互不影响地通过),它们可能在空中相遇 |
| C.若两小球同时抛出,它们不能在空中相遇 |
| D.若要使它们能在空中相遇,必须在a到达bc时将b抛出 |
如图所示,两个物体以相同大小的初始速度从O点同时分别向x轴正负方向水平抛出,它们的轨迹恰好是抛物线方程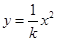 ,(曲率半径简单地理解,在曲线上一点附近与之重合的圆弧的最大半径)那么以下说法正确的是 ( )
,(曲率半径简单地理解,在曲线上一点附近与之重合的圆弧的最大半径)那么以下说法正确的是 ( )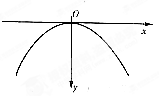
A.初始速度为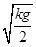 |
B.初始速度为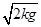 |
C.O点的曲率半径为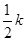 |
| D.O点的曲率半径为2k |
物体在平抛运动的过程中,在相等的时间内,下列物理量相等的是( )
| A.速度的增量 | B.加速度 | C.位移 | D.平均速度 |
某星球的质量约为地球的9倍,半径约为地球的一半,若从地球上高h处平抛一物体,射程为60m,在该星球上以同样的初速度和同样的高度平抛一物体,其射程为
| A.10m | B.15m | C.90m | D.360m |
如图所示,小球以v0正对倾角为θ的斜面水平抛出,若小球到达斜面的位移最小,则飞行时间t为(重力加速度为g)( ) 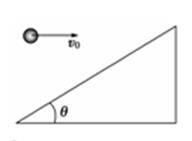
| A.v0tanθ | B.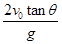 | C.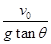 | D.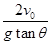 |
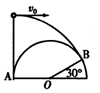
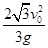
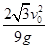
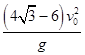
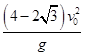
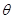 的斜面水平抛出,若小球到达斜面的位移最小,则飞行时间t为(重力加速度为g)
的斜面水平抛出,若小球到达斜面的位移最小,则飞行时间t为(重力加速度为g)