题目内容
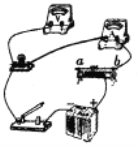
【题目】如图所示，可视为质点两物体A、B质量均为m=10kg，它们之间用可遥控引爆的粘性炸药粘连在一起，现使两物体从光滑曲面（末端切线水平）上高度H=0.8m处由静止释放，到达底端时进入水平传送带，随即撤掉光滑曲面，传送带匀速向左传动，速率为
。已知两物体与传送带间的动摩擦因数均为μ=0.1，
，按要求回到下列问题：
（1）若两物体从传送带右端滑出，求皮带轮间的距离s需满足的条件；
（2）若皮带轮间的距离足够大，求从两物体滑上离开传送带的整个过程中，由于两物体和传送带间的摩擦产生的热量Q；
（3）若两皮带轮半径r=10cm，间距为13.5m。当两物体滑上皮带后经过2s的那一时刻，用遥控器引爆粘性炸药，此后两物体分离，物体B恰好从传送带右端平抛飞出。若爆炸所用时间极短，可忽略不计，爆炸所释放的化学能80％转化为两物体的机械能，求爆炸所释放的化学能E。
【答案】（1）小于8m（2）490J（3）50J
【解析】试题分析：若不启动引爆装置，AB整体在光滑曲面上下滑时，只有重力做功，机械能守恒，由机械能守恒定律求出AB刚滑到曲面底端时的速度．研究AB在传送带上运动的过程，由动量定理求得滑行时间，再结合运动学公式求解AB在水平传送带上运动的最远距离s．根据相对位移求由于摩擦而增加的内能Q，研究AB从开始到爆炸位置的过程，由动能定理求出AB的速度．对于爆炸过程，由于内力远大于外力，所以系统的动量守恒，由动量守恒定律列式．根据B到传送带右端时对传送带无压力，分析物体B的受力情况，知道重力提供向心力，由此求出B的速度．联立可求得d。
(1) AB下滑到皮带上的速度为v，由机械能守恒定律
解得
；
设皮带轮间的距离最小值为
即皮带轮间的距离需满足的条件：
(2) 物体向右减速到零的时间为t1，物体向左加速到与皮带达到共速的时间为
，则
，
物体向右减速到零的时间内相对皮带滑行的距离为
，物体向左加速到与皮带达到同速的时间内相对皮带滑行的距离为
，则
，
则从两物体滑上到离开传送带的整个过程中，由于两物体和传送带间的摩擦产生了热量
；
（3）两物体滑上皮带后经过2s的那一时刻的速度为
,滑行的距离为x,则
物体B恰好从传送带右端平抛飞出，则物体B对应的速度
，解得
炸药爆炸后瞬间物体AB对应的速度分别为
、
，则
，解得
根据动量守恒定律
解得
爆炸后物体AB所获得的机械能为E
解得
爆炸所释放的化学能
。
点晴：对于传送带类题目要注意因摩擦产生的内能等于摩擦力与相对位移间的乘积，要准确分析物体的运动情况，抓住爆炸的基本规律：动量守恒定律。
