题目内容
如图所示,A、B、C是三个完全相同的物块,质量均为m,其中物块A、B用轻弹簧相连,将它们竖直放在水平地面上处于静止状态,此时弹簧的压缩量为x0。已知重力加速度为g,物块的厚度及空气阻力均可忽略不计,且在下面所述的各过程中弹簧形变始终在弹性限度内。
1.若用力将物块A竖直向上缓慢提起,使物块B恰好能离开水平地面,求此过程中物块A被提起的高度。
2.如果使物块C从距物块A高3x0处自由落下,C与A相碰后,立即与A粘在一起不再分开,它们运动到最低点后又向上弹起,物块A刚好能回到使弹簧恢复为原长的位置。求C与A相碰前弹簧的弹性势能大小。
3.如果将物块C从距物块A上方某处由静止释放, C与A相碰后立即一起向下运动但并不粘连。此后物块A、C在弹起过程中分离,其中物块C运动到最高点时被某装置接收,而物块A刚好能在物块B不离开地面的情况下做简谐运动。求物块C的释放位置与接收位置间的距离。
1.L= x0+ x1=2x0
2.Ep= mgx0
mgx0
3.6.5x0
【解析】
(1)设弹簧劲度系数为k,物块A、B用轻弹簧相连接,竖直放置时,弹簧被压缩,A处于平衡状态,此时弹簧压缩量 x0=mg/k
缓慢提起A到B将要离开水平地面时弹簧伸长x1,此时物块B所受重力和弹力平衡,所以弹簧伸长量 x1=mg/k= x0
物块A向上提起的高度 L= x0+ x1=2x0
(2)设C自由落下到与A相碰前的速度为v1,由机械能守恒定律有
mg·3x0= mv12
mv12
设C与A相碰后一起向下运动的初速度为v2,根据动量守恒定律有
mv1=2mv2
设C与A相碰前弹簧的弹性势能为Ep。 物块A、C运动到最低点后又向上弹起,刚好能回到使弹簧恢复为原长的位置过程中,A、C与弹簧组成的系统机械能守恒,有
 2mv22+Ep=2mgx0
2mv22+Ep=2mgx0
联立以上各式,解得:Ep= mgx0
mgx0
说明:另一解法是直接运用弹性势能公式: mg=kx0,k=mg/x0,则Ep= kx0=
kx0= mgx0
mgx0
这种解法同样得4分。
(3)设物块C释放位置到物块A的高度差为h0,与物块A碰撞前速度为v3,由机械能守恒定律有: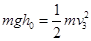
设C与A相碰后一起向下运动的初速度为v4,根据动量守恒定律有
mv3=2mv4
物块A、C一起向下压缩弹簧后向上弹起,到达弹簧原长时C与A分离,设分离时的速度为v5,对此过程由机械能守恒定律有
 2mv42+Ep=2mgx0+
2mv42+Ep=2mgx0+ 2mv52
2mv52
之后,物块C向上做匀减速运动,设上升的高度为h,则根据机械能守恒定律有
 mv52=mgh, 解得
mv52=mgh, 解得 
因物块A刚好能在物块B不离开地面的情况下做简谐运动,结合第(1)问可知,物块A运动到最高点时,弹簧形变量为x0。所以物块A运动到最高点时弹簧的弹性势能与物块A处于静止状态时弹簧的弹性势能相等。
所以对物块A从弹簧恢复原长位置运动到最高点过程中,由机械能守恒定律有
 mv52=mgx0+Ep
mv52=mgx0+Ep
联立以上各式,解得:h0=9x0,h=1.5x0。
由几何关系可知,物块C的释放位置与接收位置间的距离
Δh=h0-x0-h=6.5x0


 如图所示,a、b、c为电场中同一电场线上的三点,且b为ac的中点,a、c电势分别为φa=8V,φc=6V.下列叙述正确的是( )
如图所示,a、b、c为电场中同一电场线上的三点,且b为ac的中点,a、c电势分别为φa=8V,φc=6V.下列叙述正确的是( ) 如图所示,A、B、C、D是某匀强电场中的4个等势面,一个质子和一个α粒子(电荷量是质子的2倍,质量是质子的4倍)同时在A等势面从静止出发,向右运动,当到达D等势面时,下列说法正确的是( )
如图所示,A、B、C、D是某匀强电场中的4个等势面,一个质子和一个α粒子(电荷量是质子的2倍,质量是质子的4倍)同时在A等势面从静止出发,向右运动,当到达D等势面时,下列说法正确的是( ) 如图所示,a、b和c都是厚度均匀的平玻璃板,a和b、b和c之间的夹角都为α,一细光束由红光和蓝光组成,以入射角θ从O点射入a板,且射出c板后的两束单色光通过空气射在地面上P、Q两点,由此可知( )
如图所示,a、b和c都是厚度均匀的平玻璃板,a和b、b和c之间的夹角都为α,一细光束由红光和蓝光组成,以入射角θ从O点射入a板,且射出c板后的两束单色光通过空气射在地面上P、Q两点,由此可知( )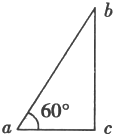 如图所示,a、b、c是匀强电场中的直角三角形的三个顶点.已知a、b、c三点的电势分别为φa=8V、φb=-4V、φc=2V,
如图所示,a、b、c是匀强电场中的直角三角形的三个顶点.已知a、b、c三点的电势分别为φa=8V、φb=-4V、φc=2V,