题目内容
8. 如图所示,穿过光滑水平平面中央小孔O的细线与平面上质量为m的小球P相连,手拉细线的另一端,让小球在水平面内以角速度ω1沿半径为a的圆周做匀速圆周运动.所有摩擦均不考虑. 求:
如图所示,穿过光滑水平平面中央小孔O的细线与平面上质量为m的小球P相连,手拉细线的另一端,让小球在水平面内以角速度ω1沿半径为a的圆周做匀速圆周运动.所有摩擦均不考虑. 求:(1)这时细线上的拉力多大?
(2)若突然松开手中的细线,经时间△t再握紧细线,随后小球沿半径为b的圆周做匀速圆周运动.试问:△t等于多大?这时的角速度ω2为多.
分析 由题意可知,小球做匀速圆周运动所需要的向心力是由细线的拉力提供的.则可求出细线上的张力大小;当突然松开手时,小球沿切线方向匀速飞出.当再次握住时,小球又做匀速圆周运动.由半径a与ω1可求出飞出之前的速度.再由半径b,结合运动的分解可求出小球以半径b做匀速圆周运动的线速度.从而可求出此时的角速度.由于是匀速飞出,所以利用直角三角形,由长度a、b可求出时间.
解答  解:(1)细线上的拉力提供向心力,根据牛顿第二定律得:$F=ma{{ω}_{1}}^{2}$
解:(1)细线上的拉力提供向心力,根据牛顿第二定律得:$F=ma{{ω}_{1}}^{2}$
(2)松开手后小球作匀速直线运动:v=aω1
时间$△t=\frac{s}{v}=\frac{\sqrt{{b}^{2}-{a}^{2}}}{a{ω}_{1}}$
小球再次作匀速圆周运动时,线使分速度v1消失,小球的速度为v2:
根据几何关系得:$sinθ=\frac{a}{b}$
v2=bω2=vsinθ
解得:
${ω}_{2}=\frac{{a}^{2}}{{b}^{2}}{ω}_{1}$
答:(1)这时细线上的拉力为$ma{{ω}_{1}}^{2}$;
(2)△t等于$\frac{\sqrt{{b}^{2}-{a}^{2}}}{a{ω}_{1}}$,这时的角速度ω2为$\frac{{a}^{2}}{{b}^{2}}{ω}_{1}$.
点评 搞清小球做匀速圆周运动所需要的向心力来源,同时本题巧妙运用三角函数求出松手前后的线速度关系.值得注意是松手后小球做的是匀速直线运动.

练习册系列答案
相关题目
19.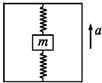 如图所示,将质量为m=0.1kg的物体用两个完全一样的竖直轻弹簧固定在升降机内,当升降机以4m/s2的加速度加速向上运动时,上面弹簧对物体的拉力为0.4N;当升降机和物体都以8m/s2的加速度向上运动时,下面弹簧对物体的支持力为( )
如图所示,将质量为m=0.1kg的物体用两个完全一样的竖直轻弹簧固定在升降机内,当升降机以4m/s2的加速度加速向上运动时,上面弹簧对物体的拉力为0.4N;当升降机和物体都以8m/s2的加速度向上运动时,下面弹簧对物体的支持力为( )
 如图所示,将质量为m=0.1kg的物体用两个完全一样的竖直轻弹簧固定在升降机内,当升降机以4m/s2的加速度加速向上运动时,上面弹簧对物体的拉力为0.4N;当升降机和物体都以8m/s2的加速度向上运动时,下面弹簧对物体的支持力为( )
如图所示,将质量为m=0.1kg的物体用两个完全一样的竖直轻弹簧固定在升降机内,当升降机以4m/s2的加速度加速向上运动时,上面弹簧对物体的拉力为0.4N;当升降机和物体都以8m/s2的加速度向上运动时,下面弹簧对物体的支持力为( )| A. | 0.6 N | B. | 0.8 N | C. | 1.0 N | D. | 1.2 N |
3.边长为a的正方形的四个顶点上放置如图所示的点电荷,则中心O处场强( )


| A. | 大小为零 | B. | 大小为$\frac{\sqrt{2}kq}{{a}^{2}}$方向沿x轴正向 | ||
| C. | 大小为$\frac{2\sqrt{2}kq}{{a}^{2}}$方向沿y轴正向 | D. | 大小为$\frac{\sqrt{2}kq}{2{a}^{2}}$方向沿y轴负向 |
17.在某次十米跳台决赛中,一选手的质量为m,她入水后受水的阻力而做减速运动,设水对她的阻力大小恒为F,当地重力加速度为g,在水中下降高度h的过程中,她的( )
| A. | 动能减少了Fh | B. | 重力势能减少了mgh | ||
| C. | 机械能减少了(F-mg)h | D. | 机械能减少了Fh |
18.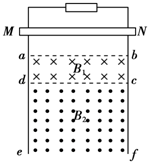 如图所示,光滑的“Π”形金属导体框竖直放置,质量为m的金属棒MN与框架接触良好,磁感应强度分别为B1、B2的有界匀强磁场方向相反,但均垂直于框架平面,分别处在abcd和cdef区域.现从图示位置由静止释放金属棒MN,金属棒进入磁场区域abcd后恰好做匀速运动.下列说法正确的有( )
如图所示,光滑的“Π”形金属导体框竖直放置,质量为m的金属棒MN与框架接触良好,磁感应强度分别为B1、B2的有界匀强磁场方向相反,但均垂直于框架平面,分别处在abcd和cdef区域.现从图示位置由静止释放金属棒MN,金属棒进入磁场区域abcd后恰好做匀速运动.下列说法正确的有( )
 如图所示,光滑的“Π”形金属导体框竖直放置,质量为m的金属棒MN与框架接触良好,磁感应强度分别为B1、B2的有界匀强磁场方向相反,但均垂直于框架平面,分别处在abcd和cdef区域.现从图示位置由静止释放金属棒MN,金属棒进入磁场区域abcd后恰好做匀速运动.下列说法正确的有( )
如图所示,光滑的“Π”形金属导体框竖直放置,质量为m的金属棒MN与框架接触良好,磁感应强度分别为B1、B2的有界匀强磁场方向相反,但均垂直于框架平面,分别处在abcd和cdef区域.现从图示位置由静止释放金属棒MN,金属棒进入磁场区域abcd后恰好做匀速运动.下列说法正确的有( )| A. | 若B2=B1,则金属棒进入cdef区域后将加速下滑 | |
| B. | 若B2=B1,则金属棒进入cdef区域后仍将保持匀速下滑 | |
| C. | 若B2<B1,则金属棒进入cdef区域后可能先加速后匀速下滑 | |
| D. | 若B2>B1,则金属棒进入cdef区域后可能先加速后匀速下滑 |

