题目内容
19．
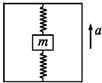如图所示，将质量为m=0.1kg的物体用两个完全一样的竖直轻弹簧固定在升降机内，当升降机以4m/s2的加速度加速向上运动时，上面弹簧对物体的拉力为0.4N；当升降机和物体都以8m/s2的加速度向上运动时，下面弹簧对物体的支持力为（ ）| A． | 0.6 N | B． | 0.8 N | C． | 1.0 N | D． | 1.2 N |
分析 根据牛顿第二定律求出升降机以4m/s2的加速度加速向上运动时，下面弹簧的弹力．然后根据牛顿第二定律求出升降机和物体都以8m/s2的加速度向上运动时，上面弹簧的拉力．
解答 解：当升降机以4m/s2的加速度加速向上运动时，设下面弹簧处于压缩，根据牛顿第二定律得，F1+F2-mg=ma1，F2=1.0N．当升降机和物体都以8m/s2的加速度向上运动时，合力F合=ma2=0.8N，根据牛顿第二定律知，两根弹簧作用在物体上的合力为1.8N，则物块要下移，根据胡克定律，两根弹簧增加的弹力相等，开始F1=0.4N，F2=1.0N，则每根弹簧增加0.2N，所以升降机和物体都以8m/s2的加速度向上运动时上面弹簧的弹力为0.6N；下面弹簧对物体的支持力为1.2N．故D正确，ABC错误．
故选：D
点评 解决本题的关键掌握牛顿第二定律以及胡克定律，知道物体下移时，两根弹簧的形变量相等，弹力变化相等．
练习册系列答案
相关题目
9．有一质量为m的木块，由碗边滑向碗底，碗内表面是半径为R的圆弧且粗糙程度不同，由于摩擦力的作用，木块的运动速率恰好保持不变，则（ ）
| A． | 它的加速度为零 | B． | 它所受合力为零 | ||
| C． | 它所受合外力大小一定，方向改变 | D． | 它所受合外力大小方向均一定 |
10．
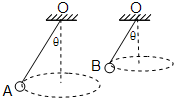小张设计了如图所示的实验，用长度不同（LOA＞LOB）细绳分别悬挂两个质量相等的小球A和B，两球在细绳作用下，分别在不同水平面内做匀速圆周运动，绳与竖直方向的夹角均为θ，则下列说法正确的是（ ）
小张设计了如图所示的实验，用长度不同（LOA＞LOB）细绳分别悬挂两个质量相等的小球A和B，两球在细绳作用下，分别在不同水平面内做匀速圆周运动，绳与竖直方向的夹角均为θ，则下列说法正确的是（ ）| A． | 线速度vA＜vB | B． | 周期TA＜TB | C． | 向心加速度aA＜aB | D． | 细绳拉力FNA=FNB |
7．关于运动的合成与分解，下列说法正确的是（ ）
| A． | 合运动的速度大小等于分运动的速度大小之和 | |
| B． | 物体的两个分运动若是直线运动，则它的合运动一定是直线运动 | |
| C． | 若合运动是曲线运动，则其分运动至少有一个是曲线运动 | |
| D． | 两个分运动是直线运动，合运动可能是直线运动，也可能是曲线运动 |
如图，在距地面高为h=0.45m处，有一小球A以初速度v=3.0m/s水平抛出，不计空气阻力，重力加速度g=10m/s2．求：
如图所示，穿过光滑水平平面中央小孔O的细线与平面上质量为m的小球P相连，手拉细线的另一端，让小球在水平面内以角速度ω1沿半径为a的圆周做匀速圆周运动．所有摩擦均不考虑． 求：
9．
在做“用单摆测定重力加速度”的实验中．
（1）如果测得的g值偏大，可能的原因是D（填写字母代号）
A．测摆长时，忘记了摆球的半径
B．摆线上端悬点未固定牢，摆动中出现松动，使摆线长度增加了
C．开始计时时，秒表过早按下
D．实验中误将49次全振动次数记为50次
（2）某同学在实验中，测量6种不同摆长l情况下单摆的振动周期T，记录实验数据如下：
请以l为横坐标，T2为纵坐标，在如图1中作出T2-l图线，并利用此图线得重力加速度g=9.86m/s2．（取π2=9.86，结果保留三位有效数字）
（3）一位同学查阅资料得知，单摆在最大摆角θ较大时周期公式可近似表述为T=2π（1+$\frac{1}{4}$sin2$\frac{θ}{2}$）$\sqrt{\frac{l}{g}}$．为了用图象法验证单摆周期T和最大摆角θ的关系，他测出摆长为l的同一单摆在不同最大摆角θ时的周期T，并根据实验数据描绘出如图2所示的图线．根据所给周期公式可知，图中的纵轴表示的是sin2$\frac{θ}{2}$，图线延长后与横轴交点的横坐标为$2π\sqrt{\frac{l}{g}}$．
在做“用单摆测定重力加速度”的实验中．（1）如果测得的g值偏大，可能的原因是D（填写字母代号）
A．测摆长时，忘记了摆球的半径
B．摆线上端悬点未固定牢，摆动中出现松动，使摆线长度增加了
C．开始计时时，秒表过早按下
D．实验中误将49次全振动次数记为50次
（2）某同学在实验中，测量6种不同摆长l情况下单摆的振动周期T，记录实验数据如下：
| l/m | 0.4 | 0.5 | 0.8 | 0.9 | 1.0 | 1.2 |
| T/s | 1.26 | 1.42 | 1.79 | 1.90 | 2.00 | 2.20 |
| T2/s2 | 1.59 | 2.02 | 3.20 | 3.61 | 4.00 | 4.84 |
（3）一位同学查阅资料得知，单摆在最大摆角θ较大时周期公式可近似表述为T=2π（1+$\frac{1}{4}$sin2$\frac{θ}{2}$）$\sqrt{\frac{l}{g}}$．为了用图象法验证单摆周期T和最大摆角θ的关系，他测出摆长为l的同一单摆在不同最大摆角θ时的周期T，并根据实验数据描绘出如图2所示的图线．根据所给周期公式可知，图中的纵轴表示的是sin2$\frac{θ}{2}$，图线延长后与横轴交点的横坐标为$2π\sqrt{\frac{l}{g}}$．