题目内容
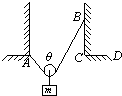 如图所示,将一根不可伸长、柔软的轻绳两端分别系于A、B两点上,一物体用动滑轮悬挂在绳子上,达到平衡时,两段绳子间的夹角为θ1,绳子中张力为T1,将绳子一端由B点移至C点,待整个系统重新达到平衡时,两段绳子间的夹角为θ2,绳子中张力为T2;再将绳子一端由C点移至D点,待整个系统再次达到平衡时,两段绳子间的夹角为θ3,绳子中张力为T3,不计摩擦,则
如图所示,将一根不可伸长、柔软的轻绳两端分别系于A、B两点上,一物体用动滑轮悬挂在绳子上,达到平衡时,两段绳子间的夹角为θ1,绳子中张力为T1,将绳子一端由B点移至C点,待整个系统重新达到平衡时,两段绳子间的夹角为θ2,绳子中张力为T2;再将绳子一端由C点移至D点,待整个系统再次达到平衡时,两段绳子间的夹角为θ3,绳子中张力为T3,不计摩擦,则
- A.θ1=θ2=θ3
- B.θ1<θ2<θ3
- C.T1>T2>T3
- D.T1=T2<T3
D
分析:绳子右端从B移动到C点时,根据几何关系可以判断出,两个绳子之间的夹角不变,然后根据三力平衡条件判断出绳子拉力不变;绳子右端从B移动到D点时,绳子间夹角变大,再次根据共点力平衡条件判断.
解答: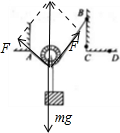 解:设绳子结点为O,对其受力分析,如图
解:设绳子结点为O,对其受力分析,如图
当绳子右端从B移动到C点时,根据几何关系,有
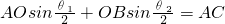
同理:AO′sin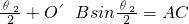
绳子长度不变,有
AO+OB=AO′+O′B
故θ1=θ2
绳子的结点受重力和两个绳子的拉力,由于绳子夹角不变,根据三力平衡可知,绳子拉力不变,即T1=T2;
绳子右端从B移动到D点时,绳子间夹角显然变大,绳子的结点受重力和两个绳子的拉力,再次根据共点力
平衡条件可得T1<T3
故D正确,A、B、C错误.
故选D.
点评:题关键根据几何关系判断出两次移动过程中两绳子间夹角的变化情况,然后根据共点力平衡条件作图,运用合成法分析.
分析:绳子右端从B移动到C点时,根据几何关系可以判断出,两个绳子之间的夹角不变,然后根据三力平衡条件判断出绳子拉力不变;绳子右端从B移动到D点时,绳子间夹角变大,再次根据共点力平衡条件判断.
解答:
 解:设绳子结点为O,对其受力分析,如图
解:设绳子结点为O,对其受力分析,如图当绳子右端从B移动到C点时,根据几何关系,有
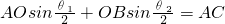
同理:AO′sin
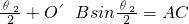
绳子长度不变,有
AO+OB=AO′+O′B
故θ1=θ2
绳子的结点受重力和两个绳子的拉力,由于绳子夹角不变,根据三力平衡可知,绳子拉力不变,即T1=T2;
绳子右端从B移动到D点时,绳子间夹角显然变大,绳子的结点受重力和两个绳子的拉力,再次根据共点力
平衡条件可得T1<T3
故D正确,A、B、C错误.
故选D.
点评:题关键根据几何关系判断出两次移动过程中两绳子间夹角的变化情况,然后根据共点力平衡条件作图,运用合成法分析.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,将一根不可伸长、柔软的轻绳两端分别系于A、B两点上,一物体用动滑轮悬挂在绳子上,达到平衡时,两段绳子间的夹角为θ1,绳子中张力为T1,将绳子一端由B点移至C点,待整个系统重新达到平衡时,两段绳子间的夹角为θ2,绳子中张力为T2;再将绳子一端由C点移至D点,待整个系统再次达到平衡时,两段绳子间的夹角为θ3,绳子中张力为T3,不计摩擦,则( )
如图所示,将一根不可伸长、柔软的轻绳两端分别系于A、B两点上,一物体用动滑轮悬挂在绳子上,达到平衡时,两段绳子间的夹角为θ1,绳子中张力为T1,将绳子一端由B点移至C点,待整个系统重新达到平衡时,两段绳子间的夹角为θ2,绳子中张力为T2;再将绳子一端由C点移至D点,待整个系统再次达到平衡时,两段绳子间的夹角为θ3,绳子中张力为T3,不计摩擦,则( ) (2008?盐城模拟)如图所示,将一根不可伸长、柔软的轻绳两端分别系于A、B两点,一物体用动滑轮悬挂在绳子上,达到平衡时,两段绳子间夹角为θ1,绳子张力为F1;将绳子B端移至C点,等整个系统达到平衡时,两段绳子间的夹角为θ2,绳子张力为F2;将绳子B端移至D点,待整个系统达到平衡时,两段绳子间的夹角为θ3,绳子张力为F3,不计摩擦,则( )
(2008?盐城模拟)如图所示,将一根不可伸长、柔软的轻绳两端分别系于A、B两点,一物体用动滑轮悬挂在绳子上,达到平衡时,两段绳子间夹角为θ1,绳子张力为F1;将绳子B端移至C点,等整个系统达到平衡时,两段绳子间的夹角为θ2,绳子张力为F2;将绳子B端移至D点,待整个系统达到平衡时,两段绳子间的夹角为θ3,绳子张力为F3,不计摩擦,则( ) 如图所示,将一根不可伸长的、柔软的轻绳左、右两端分别系于A,B两点上,一物体用动滑轮悬挂在轻绳上,达到平衡时,两段绳子间的夹角为θ1,绳子张力为F1;将绳子右端移至C点,待系统达到平衡时,两段绳子间的夹角为θ2,绳子张力为F2;将绳子右端再由C点移至D点,待系统达到平衡时,两段绳子间的夹角为θ3,绳子张力为F3,不计摩擦,并且BC为竖直线,则( )
如图所示,将一根不可伸长的、柔软的轻绳左、右两端分别系于A,B两点上,一物体用动滑轮悬挂在轻绳上,达到平衡时,两段绳子间的夹角为θ1,绳子张力为F1;将绳子右端移至C点,待系统达到平衡时,两段绳子间的夹角为θ2,绳子张力为F2;将绳子右端再由C点移至D点,待系统达到平衡时,两段绳子间的夹角为θ3,绳子张力为F3,不计摩擦,并且BC为竖直线,则( ) 如图所示,将一根不可伸长的柔软轻绳的两端系在两根立于水平地面上的竖直杆M、N等高的两点a、b上,用一个动滑轮(不计摩擦)悬挂一个重物G后挂在绳子上,达到平衡时,两段绳子的拉力为T1,现将绳子b端慢慢向下移动一段距离,待系统再次达到平衡时,两绳子的拉力为T2,则( )
如图所示,将一根不可伸长的柔软轻绳的两端系在两根立于水平地面上的竖直杆M、N等高的两点a、b上,用一个动滑轮(不计摩擦)悬挂一个重物G后挂在绳子上,达到平衡时,两段绳子的拉力为T1,现将绳子b端慢慢向下移动一段距离,待系统再次达到平衡时,两绳子的拉力为T2,则( )
 B.
B. C.F1>F2>F3 D.F1=F2<F3
C.F1>F2>F3 D.F1=F2<F3