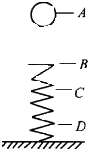题目内容
【题目】一直角轻杆两边等长.两端分别固定质量为m1的小球A和质量为m2的小球B,质量关系为 ![]() ,轻杆能绕水平转轴O在竖直面内转动,现使OB水平,如图所示,两小球从静止开始运动,经过一段时间轻杆转过θ角.不计转轴摩擦和空气阻力,两小球可视为质点,下列说法正确的是( )
,轻杆能绕水平转轴O在竖直面内转动,现使OB水平,如图所示,两小球从静止开始运动,经过一段时间轻杆转过θ角.不计转轴摩擦和空气阻力,两小球可视为质点,下列说法正确的是( )
A.θ角最大可达到150°
B.当θ=90°时,两小球速度最大
C.当θ=30°时,两小球速度最大
D.当θ=60°时,两小球速度最大
【答案】D
【解析】解:系统机械能守恒,减小的重力势能等于增加的动能,有
m2gLsinθ﹣m1gL(1﹣cosθ)= ![]()
![]()
解得
v= ![]()
故当θ=60°时,速度有最大值;当θ=120°时,速度又减为零;
故选D.
【考点精析】认真审题,首先需要了解机械能守恒及其条件(在只有重力(和弹簧弹力)做功的情形下,物体动能和重力势能(及弹性势能)发生相互转化,但机械能的总量保持不变).

 名校课堂系列答案
名校课堂系列答案【题目】某实验小组欲以图甲所示实验装置“探究加速度与物体受力和质量的关系”.图中A为小车,B为装有砝码的小盘,C为一端带有定滑轮的长木板,小车通过纸带与电磁打点计时器相连,小车的质量为m1,小盘(及砝码)的质量为m2.
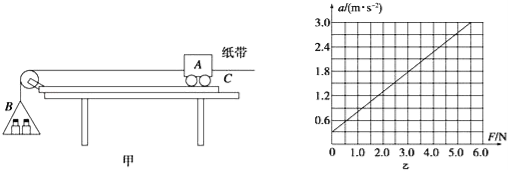
(1)下列说法正确的是 .
A.实验时先放开小车,再接通打点计时器的电源 |
B.每次改变小车质量时,应重新平衡摩擦力 |
C.本实验中应满足m2远小于ml的条件 |
D.在用图象探究小车加速度与受力的关系时,应作a﹣ml图象 |
(2)某同学平衡好摩擦阻力后,在保持小车质量不变的情况下,通过多次改变砝码重力,作出小车加速度a 与砝码重力F的图象如图乙所示.若牛顿第二定律成立,重力加速度g=10m/s2,则小车的质量为 kg,小盘的质量为 kg.
(3)实际上,在砝码的重力越来越大时,小车的加速度不能无限制地增大,将趋近于某一极限值,此极限值为 m/s2.