题目内容
如图所示，斜面体B静置于水平桌面上．一质量为m的木块A从斜面底端开始以初速度v0沿斜面上滑，然后又返回出发点，此时速度为v，且v＜v0．在上述过程中斜面体一直没有移动，由此可以得出（ ）分析：对A进行受力分析，由牛顿第二定律判断加速度的大小，由滑动摩擦力公式判断A受到的滑动摩擦力如何变化；
对物体B受力分析，然后根据平衡条件分析答题．
对物体B受力分析，然后根据平衡条件分析答题．
解答：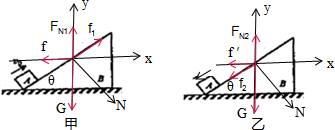
解：由于v＜v0，所以物体A在在滑动过程中受到滑动摩擦力作用；物体A受到的滑动摩擦力fA=μmgcosθ，
物体A受到的摩擦力与A对B的摩擦力是作用力与反作用力，故f1=f2=fA=μmgcosθ，对斜面体B进行受力分析，物体A向上滑动时，B受力如图甲所示，物体A向下滑动时，斜面体受力如图B所示；
A、上滑时，a1=
=gsinθ+μgcosθ，下滑时，a2=
=gsinθ-μgcosθ，所以a1＞a2，故A错误；
B、物体B处于平衡状态，由平衡条件得：FN1=G+Ncoθ-f1sinθ，FN2=G+Ncosθ+f2sinθ，FN2＞FN1，故BC错误；
D、物体B静止，处于平衡条件，由平衡条件得：f=f1cosθ+Nsinθ，f′=Nsinθ-f2cosθ，
物体A向上滑行时桌面对B的摩擦力大，物体A下滑时，桌面对B的摩擦力小，故D正确；
故选D
解：由于v＜v0，所以物体A在在滑动过程中受到滑动摩擦力作用；物体A受到的滑动摩擦力fA=μmgcosθ，物体A受到的摩擦力与A对B的摩擦力是作用力与反作用力，故f1=f2=fA=μmgcosθ，对斜面体B进行受力分析，物体A向上滑动时，B受力如图甲所示，物体A向下滑动时，斜面体受力如图B所示；
A、上滑时，a1=
| mgsinθ+μmgcosθ |
| m |
| mgsinθ-μmgcosθ |
| m |
B、物体B处于平衡状态，由平衡条件得：FN1=G+Ncoθ-f1sinθ，FN2=G+Ncosθ+f2sinθ，FN2＞FN1，故BC错误；
D、物体B静止，处于平衡条件，由平衡条件得：f=f1cosθ+Nsinθ，f′=Nsinθ-f2cosθ，
物体A向上滑行时桌面对B的摩擦力大，物体A下滑时，桌面对B的摩擦力小，故D正确；
故选D
点评：对物体正确受力分析、熟练应用平衡条件是正确解题的关键；解题时要注意受力分析的顺序，先对A受力分析，然后再对B受力分析．
练习册系列答案
相关题目
（2011?长沙模拟）如图所示，斜面体B静置于水平桌面上．一质量为m的木块A从斜面底端开始以初速度v0上滑，然后又返回出发点，此时速度为v，且v＜v0．在上述过程中斜面体一直静止不动，以下说法正确的是（ ）
如图所示，斜面体B静置于水平桌面上．一质量为m的木块A从斜面底端开始以初速度v0沿斜面上滑，然后又返回出发点，此时速度为v，且v＜v0．在上述过程中斜面体一直没有移动，则地面对斜面体B的摩擦力（ ）
如图所示，斜面体B静置于水平桌面上，一质量为m的木块A从斜面底端开始以大小为V0的初速度沿斜面（足够长）向上滑，然后又返回出发点，返回到底端时的速度大小为V，且V＜V0．上述过程中斜面体没有移动，由此可得出的结论是（ ）
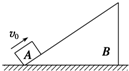如图所示，斜面体B静置于水平桌面上．一质量为M的木块A从斜面底端开始以初速度v0上滑，然后又返回出发点，此时速度为v，且v＜v0．在上述过程中斜面体一直静止不动，以下说法正确的是（ ）| A、滑块向上运动过程中处于超重状态，在下滑过程中处于失重状态 | B、A上滑时比下滑时桌面对B的支持力小 | C、滑块上滑过程中机械能减小，下滑过程中机械能增大 | D、桌面对B始终有水平向左的静摩擦力 |