题目内容
如图所示，AB为斜轨道，与水平方向成45°角，BC为水平轨道，两轨道在B处通过一段小圆弧相连接，一个质量为m的小物块，自轨道AB的A处从静止开始沿轨道下滑，最后停在轨道上的C点，已知A点高h，物块与轨道间的动摩擦因数为μ，求：物块沿轨道AB段与轨道BC段滑动的时间之比值t1 ∶t2 ．
（16分） 解：设物块沿轨道AB滑动的加速度为a1，由牛顿第二定律，有mgsin45°－μmgcos45°＝ma1． ① （3分）设物块沿轨道B点时的速率为vB，则有vB＝a1t1． ② （3分）设物块沿轨道BC滑动的加速度为a2，由牛顿第二定律，有μmg＝ma2． ③ （3分）物块从B点开始做匀减直线运动，到达C点时，速度为零，故有0＝vB－a2t2． ④ （3分）由①、②、③、④各式得＝＝． （4分）
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
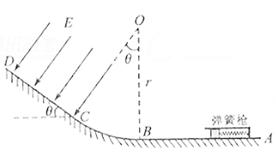
（2012?四川）如图所示，ABCD为固定在竖直平面内的轨道，AB段光滑水平，BC段为光滑圆弧，对应的圆心角θ=370，半径r=2.5m，CD段平直倾斜且粗糙，各段轨道均平滑连接，倾斜轨道所在区域有场强大小为E=2×l05N/C、方向垂直于斜轨向下的匀强电场．质量m=5×l0-2kg、电荷量q=+1×10-6C的小物体（视为质点）被弹簧枪发射后，沿水平轨道向左滑行，在C点以速度v0=3m/s冲上斜轨．以小物体通过C点时为计时起点，0.1s以后，场强大小不变，方向反向．已知斜轨与小物体间的动摩擦因数μ=0.25．设小物体的电荷量保持不变，取g=10m/s2．sin37°=0.6，cos37°=0.8．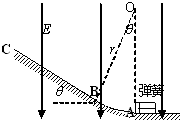
如图所示，ABC为固定在竖直平面内的轨道，AB段为光滑圆弧，对应的圆心角θ=37°，OA竖直，半径r=2.5m，BC为足够长的平直倾斜轨道，倾角θ=37°．已知斜轨BC与小物体间的动摩擦因数μ=0.25．各段轨道均平滑连接，轨道所在区域有E=4×103N/C、方向竖直向下的匀强电场．质量m=5×10-2kg、电荷量q=+1×10-4C的小物体（视为质点）被一个压紧的弹簧发射后，沿AB圆弧轨道向左上滑，在B点以速度v0=3m/s冲上斜轨．设小物体的电荷量保持不变．重力加速度g=10m/s2，sin37°=0.6，cos37°=0.8．（设弹簧每次均为弹性形变．）
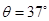，半径r=2.5m，CD段平直倾斜且粗糙，各段轨道均平滑连接，倾斜轨道所在区域有场强大小为
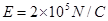、方向垂直于余轨向下的匀强电场。质量
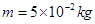、电荷量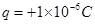
的小物体（视为质点）被弹簧枪发射后，沿水平轨道向左滑行，在C点以速度
冲上斜轨。以小物体通过C点时为计时起点，0.1s以后，场强大小不变，方向反向。已知斜轨与小物体间的动摩擦因数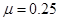
。设小物体的电荷量保持不变，取
，
。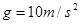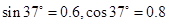