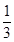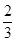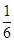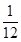题目内容
(15分)如图所示，在宽度为L的两虚线区域内存在匀强电场，一质量为m，带电量为＋q的滑块(可看成点电荷)，从距该区域为L的绝缘水平面上以初速度v0向右运动并进入电场区域，滑块与水平面间的动摩擦因数为μ。
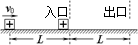
⑴若该区域电场为水平方向，并且用速度传感器测得滑块从出口处滑出的速度与进入该区域的速度相同，求该区域的电场强度大小与方向，以及滑块滑出该区域的速度；
⑵若该区域电场为水平方向，并且用速度传感器测得滑块滑出该区域的速度等于滑块的初速度v0，求该区域的电场强度大小与方向；
⑶若将该区域电场改为竖直方向，测出滑块到达出口处速度为v0/2(此问中取v0＝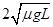
)，再将该区域电场反向后，发现滑块未能从出口滑出，求滑块所停位置距左边界多远。
⑴若该区域电场为水平方向，并且用速度传感器测得滑块从出口处滑出的速度与进入该区域的速度相同，求该区域的电场强度大小与方向，以及滑块滑出该区域的速度；
⑵若该区域电场为水平方向，并且用速度传感器测得滑块滑出该区域的速度等于滑块的初速度v0，求该区域的电场强度大小与方向；
⑶若将该区域电场改为竖直方向，测出滑块到达出口处速度为v0/2(此问中取v0＝
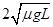)，再将该区域电场反向后，发现滑块未能从出口滑出，求滑块所停位置距左边界多远。 ⑴E＝
，方向水平向右，v＝
；⑵E＝
，方向水平向右；⑶s＝
，方向水平向右，v＝；⑵E＝，方向水平向右；⑶s＝试题分析：⑴滑块从出口处滑出的速度与进入该区域的速度相同，说明滑块在电场区域匀速运动，根据平衡条件有：qE＝μmg，解得：E＝
，其方向水平向右滑块进入电场前，根据动能定理有：－μmgL＝
－
解得滑块滑出该区域的速度为：v＝
⑵从滑块开始运动到出电场区域，根据动能定理有：－2μmgL＋qEL＝
－解得：E＝
，其方向水平向右⑶根据题意可以判断出，第一次时电场方向为竖直向上，根据动能定理有：－μmgL－μ(mg－qE)L＝
－第二次电场反向后，设滑块所停位置距左边界距离为s，根据动能定理有：－μmgL－μ(mg＋qE)L＝0－
又因为v0＝
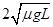
联立解得：s＝
练习册系列答案
课堂全解字词句段篇章系列答案
相关题目
10－4C。与水平的轨道之间的滑动摩擦系数m= 0.2，在一个水平向左的匀强电场中，E = 4
，方向垂直纸面向里，问能否运动到L点？（回答：“能”或“不能”即可）如果小物块最后能落回到水平面MN上，则刚到达MN时小物块的速度大小为多少？
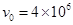m/s沿AB方向从A点进入电场，恰好穿过孔O1和O2后，从H点离开电场。金属板间的距离L1＝2 cm，L2＝4 cm，L3＝6 cm。电子质量
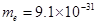kg，电荷量
C。正对的两平行板间可视为匀强电场，求：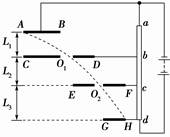
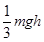；木块通过 B 点后继续滑行2h 距离后，在 C 点停下来，则木块与曲面间的动摩擦因数应为
