题目内容
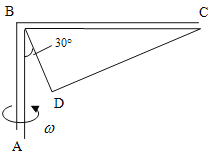
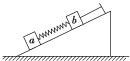
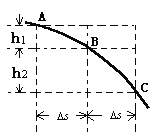
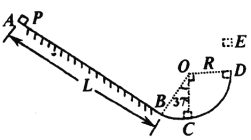
【题目】如图所示,粗糙的斜面AB下端与光滑的圆弧轨道BCD相切于B,整个装置竖直放置,C是最低点,圆心角∠BOC为θ=37°,D与圆心O等高,圆弧轨道半径R=1.0m,斜面长L=4.0m,现有一个质量m=1.0kg的小物体P从斜面AB上端A点无初速下滑,物体P与斜面AB之间的动摩擦因数为μ=0.25,g取10m/s2,sin37°=0.6,cos37°=0.8,不计空气阻力.求:
(1)物体P第一次通过C点时的速度vC大小;
(2)物体P第一次离开D点后在空中做竖直上抛运动,则最高点E和D点之间的高度差h为多大?(3)物体P从A点无初速下滑后的整个过程中,在斜面上运动的总路程s为多少?在轨道上C点所受的最小支持力N是多大?
【答案】(1)![]() m/s (2) h=0.8m (3) S=11m N=14N
m/s (2) h=0.8m (3) S=11m N=14N
【解析】
(1)由几何关系可判断斜面与水平面的夹角也为θ=37°,物体P从A下滑经B到C过程中根据动能定理有:
mg(Lsin37°+R-Rcos37°)-μmgLcos37°=![]() m
m![]()
得:![]() =
=![]()
代入数据得![]() =6m/s
=6m/s
(2)从C到E机械能守恒有:mg(R+h)=![]() m
m![]()
E与D间高度差为:h=![]() -R,代入数据得E和D点之间的高度差h=0.8m
-R,代入数据得E和D点之间的高度差h=0.8m
(3)物体P最后在B与其等高的圆弧轨道上来回运动时,经C点压力最小,,设在C点的最小速度为v,由B到C根据机械能守恒有:
mgR(1-cos37°)=![]() m
m![]()
v=![]() =2m/s
=2m/s
在C点所受的最小支持力N:N-mg=m![]() ,N=mg+m
,N=mg+m![]()
代入数据得N=14N
由动能定理可得P在斜面上运动的总路程S:
mgLsin37°-μmgScos37°=![]() m
m![]() -0
-0
代入数据得S=11m

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案【题目】某学习小组想测量一种导电溶液的电阻率,先在一根均匀的长玻璃管两端各装了一个电极 (接触电阻不计),两电极相距 L=0.700m,玻璃管的内径为 d=4.000mm,其间充满待测的导电溶液。实验所用器材如下:
电压表(量程 15V,内阻约 30kΩ); 电流表(量程 300μA,内阻约 50Ω); 滑动变阻器(100Ω,0.1A);
电池组(电动势 E=12V,内阻约 6Ω);
单 刀 单 掷 开 关 一 个 ;
导 线 若 干 。
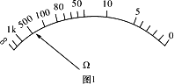
(1)该小组先用欧姆表粗测溶液电阻,他们选择欧姆×100 挡,欧姆调零后测量结果如图 1 所示,为了使读数更精确些,接下来要进行的步骤是_________。
A.换为×10 挡,不重新欧姆调零就测量
B.换为×1k挡,不重新欧姆调零就测量
C.换为×10 挡,重新欧姆调零后再测量
D.换为×1k挡,重新欧姆调零后再测量
(2)根据欧姆表的粗测结果及可供选择的器材,学习小组设计了实验电路,下表是他们测量的数据。
U/V | 0 | 1.0 | 3.0 | 5.0 | 7.0 | 9.0 | 11.0 |
I/μA | 0 | 22 | 65 | 109 | 155 | 175 | 240 |
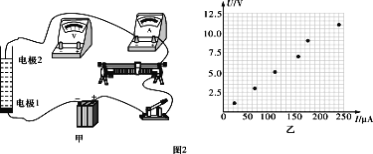
由以上信息,你认为该研究小组设计的电路图是以下选项中的________,并根据电路图将图 2 甲实物图连线补充完整。
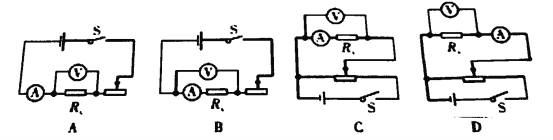
(3)根据表中数据在坐标图中已描点,请你在图 2 乙上作出U-I 图象,并根据图象求出电阻
R=_____Ω(保留两位有效数字)测量导电溶液的电阻率的表达式 ρ=________ (用题给物理量的符号表示)。