题目内容
如图（a）所示，光滑水平面上停放着一辆上表面粗糙的平板车，质量为M，车的上表面距地面的高度与车上表面长度相同．一质量为m的铁块以水平初速度v0滑到小车上，它们的速度随时间变化的图象如图（b）所示（t0是滑块在车上运动的时间），重力加速度为g．则下列判断正确的是（ ）分析：根据图线知，铁块在小车上滑动过程中，铁块做匀减速直线运动，小车做匀加速直线运动．根据牛顿第二定律通过它们的加速度之比求出质量之比，以及求出动摩擦因数的大小．根据运动学公式分别求出铁块和小车的位移，从而求出两者的相对位移，即平板车的长度．物体离开小车做平抛运动，求出落地的时间，从而根据运动学公式求出物体落地时与车左端的位移．
解答：解：A、根据图线知，铁块的加速度大小a1=
=
．小车的加速度大小a2=
，知铁块与小车的加速度之比为2：3，根据牛顿第二定律，铁块的加速度a1=
，小车的加速度a2=
，则铁块与小车的质量之比m：M=3：2．故A错误．
B、铁块的加速度a1=
=μg，又a1=
，则μ=
．故B正确．
C、铁块的位移x1=
t0=
v0t0，小车的位移x2=
t0=
，则小车的长度L=
-
=
．故C正确．
D、物体离开小车做平抛运动，运动时间t=
，则铁块距小车左端的距离△x=(
v0+
)t=
．故D错误．
故选BC．
v0-
| ||
| t0 |
| v0 |
| 3t0 |
| v0 |
| 2t0 |
| f |
| m |
| f |
| M |
B、铁块的加速度a1=
| f |
| m |
| v0 |
| 3t0 |
| v0 |
| 3gt0 |
C、铁块的位移x1=
v0+
| ||
| 2 |
| 5 |
| 6 |
| ||
| 2 |
| v0t0 |
| 4 |
| 5v0t0 |
| 6 |
| v0t0 |
| 4 |
| 7v0t0 |
| 12 |
D、物体离开小车做平抛运动，运动时间t=
|
| 2 |
| 3 |
| v0 |
| 2 |
| 7v0 |
| 6 |
|
故选BC．
点评：解决本题的关键理清小车和铁块的运动情况，结合牛顿第二定律和运动学公式进行求解．
练习册系列答案
走进文言文系列答案
相关题目
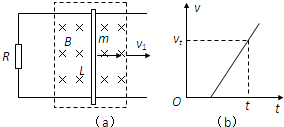（2007?上海）如图（a）所示，光滑的平行长直金属导轨置于水平面内，间距为L、导轨左端接有阻值为R的电阻，质量为m的导体棒垂直跨接在导轨上．导轨和导体棒的电阻均不计，且接触良好．在导轨平面上有一矩形区域内存在着竖直向下的匀强磁场，磁感应强度大小为B．开始时，导体棒静止于磁场区域的右端，当磁场以速度v1匀速向右移动时，导体棒随之开始运动，同时受到水平向左、大小为f的恒定阻力，并很快达到恒定速度，此时导体棒仍处于磁场区域内．
