题目内容
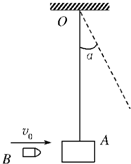 一根轻绳长L=1.6m,一端系在固定支架上,另一端悬挂一个质量为M=1kg的沙箱A,沙箱处于静止.质量为m=10g的子弹B以水平速度v0=500m/s射入沙箱,其后以水平速度v=100m/s从沙箱穿出(子弹与沙箱相互作用时间极短).g=10m/s2.求:
一根轻绳长L=1.6m,一端系在固定支架上,另一端悬挂一个质量为M=1kg的沙箱A,沙箱处于静止.质量为m=10g的子弹B以水平速度v0=500m/s射入沙箱,其后以水平速度v=100m/s从沙箱穿出(子弹与沙箱相互作用时间极短).g=10m/s2.求:(1)子弹射出沙箱瞬间,沙箱的速度u的大小;
(2)沙箱和子弹作为一个系统共同损失的机械能E损;
(3)沙箱摆动后能上升的最大高度h;
(4)沙箱从最高点返回到最低点时,绳对箱的拉力F的大小.
分析:(1)子弹打木块过程动量守恒,据此列方程即可正确求解.
(2)根据功能关系,求出系统作用前后损失的动能即为损失的机械能.
(3)子弹打完沙箱,沙箱摆动过程中机械能守恒,据此列方程即可求解.
(4)在最低点根据向心力公式列方程,即可求出绳对箱的拉力大小.
(2)根据功能关系,求出系统作用前后损失的动能即为损失的机械能.
(3)子弹打完沙箱,沙箱摆动过程中机械能守恒,据此列方程即可求解.
(4)在最低点根据向心力公式列方程,即可求出绳对箱的拉力大小.
解答:解:(1)子弹穿过沙箱的过程中动量守恒,据此有:
mv0=Mu+mv,代入数据求得:μ=4m/s.
故沙箱的速度为4m/s.
(2)根据功能关系,系统损失的机械能为:
△E=
m
-
mv2-
Mu2,代入数据得:△E=1192J.
故系统损失的机械能为1192J.
(3)沙箱摆动过程中,机械能守恒,所以有:Mgh=
Mu2,解得:h=0.8m.
故沙箱摆动后能上升的最大高度h=0.8m.
(4)根据机械能守恒可知,当沙箱返回到最低点时,速度大小仍为u=4m/s,因此有:
F-Mg=M
,所以解得:F=20N.
故沙箱从最高点返回到最低点时,绳对箱的拉力F的大小为20N.
mv0=Mu+mv,代入数据求得:μ=4m/s.
故沙箱的速度为4m/s.
(2)根据功能关系,系统损失的机械能为:
△E=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
| 1 |
| 2 |
故系统损失的机械能为1192J.
(3)沙箱摆动过程中,机械能守恒,所以有:Mgh=
| 1 |
| 2 |
故沙箱摆动后能上升的最大高度h=0.8m.
(4)根据机械能守恒可知,当沙箱返回到最低点时,速度大小仍为u=4m/s,因此有:
F-Mg=M
| u2 |
| L |
故沙箱从最高点返回到最低点时,绳对箱的拉力F的大小为20N.
点评:本题比较简单,考查了动量守恒、机械能守恒等基本规律的应用,解题过程中注意公式、定理的使用条件.

练习册系列答案
相关题目
 如图所示,长L的均匀长杆AB,质量为m,A端用光滑转轴与竖直墙壁相连,另一端B与一根轻质细绳相连,绳的另一端通过一个光滑小定滑轮与一个放置在杆上的、质量也是m的物体C相连接,物体和杆都处于静止状态,且BC=
如图所示,长L的均匀长杆AB,质量为m,A端用光滑转轴与竖直墙壁相连,另一端B与一根轻质细绳相连,绳的另一端通过一个光滑小定滑轮与一个放置在杆上的、质量也是m的物体C相连接,物体和杆都处于静止状态,且BC= 如图所示,长L的均匀长杆AB,质量为m,A端用光滑转轴与竖直墙壁相连,另一端B与一根轻质细绳相连,绳的另一端通过一个光滑小定滑轮与一个放置在杆上的、质量也是m的物体C相连接,物体和杆都处于静止状态,且BC=
如图所示,长L的均匀长杆AB,质量为m,A端用光滑转轴与竖直墙壁相连,另一端B与一根轻质细绳相连,绳的另一端通过一个光滑小定滑轮与一个放置在杆上的、质量也是m的物体C相连接,物体和杆都处于静止状态,且BC=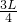 ,DC⊥AB. 已知重力加速度为g,sin37°=0.6,cos37°=0.8.试求:
,DC⊥AB. 已知重力加速度为g,sin37°=0.6,cos37°=0.8.试求:



 两点的相对距离不变,相对运动轨迹为圆弧,VA=VB+VAB,在AB连线上
两点的相对距离不变,相对运动轨迹为圆弧,VA=VB+VAB,在AB连线上





 =
= 
















