题目内容
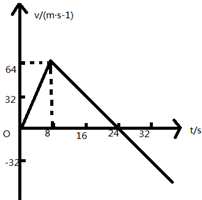 一宇宙空间探测器从某一星球表面竖直升空,宇宙探测器升到空中某一高度,发动机关闭,其速度随时间的变化关系如图所示.
一宇宙空间探测器从某一星球表面竖直升空,宇宙探测器升到空中某一高度,发动机关闭,其速度随时间的变化关系如图所示.
(1)升空后8秒末,24秒末,32秒末探测器的速度分别是多少?
(2)探测器哪一时刻关闭发动机?哪一时刻达到最大高度?哪一时刻开始下降?
(3)探测器所能达到的最大高度是多少?
(4)求探测器加速上升的过程中加速度?求下降过程的加速度?
解:(1)升空后,8s末探测器的速度为v1=64m/s,24s末速度为v2=0,32s末速度为v3=-32m/s.
(2)探测器在t=8s末关闭发动机,在t=24s末到达最大高度,t=24s开始下降.
(3)由速度图象的“面积”大小等于位移,则得探测器所能达到的最大高度为
H=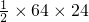 m=768m
m=768m
(4)在0-24s时间内探测器上升,则上升过程的加速度为
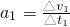 =
=
在24s后探测器开始下降,则下降过程的加速度为
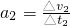 =
=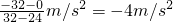
答:(1)升空后8秒末,24秒末,32秒末探测器的速度分别是64m/s,0和-32m/s.
(2)探测器8s末时刻关闭发动机,24s末时刻达到最大高度,24s末时刻开始下降.
(3)探测器所能达到的最大高度是768m.
(4)探测器加速上升的过程中加速度是8m/s2,下降过程的加速度是-4m/s2.
分析:(1)由图直接读出速度;
(2)(3)探测器先向上做匀加速运动,关闭发动机后,探测器先向上做匀减速运动,后向下做匀加速运动,由图可读出t=8s末关闭发动机.匀减速运动速度减小至零时,到达最大高度,由速度图象的“面积”大小等于位移求出最大高度.在=24s末探测器开始下落;
(4)根据速度图象的斜率等于加速度,求出加速上升和下降过程的加速度.
点评:本题通过分析探测器的运动情况,判断关闭发动机的时刻,根据“面积”大小求出最大高度,根据斜率求解加速度,都是常规问题.
(2)探测器在t=8s末关闭发动机,在t=24s末到达最大高度,t=24s开始下降.
(3)由速度图象的“面积”大小等于位移,则得探测器所能达到的最大高度为
H=
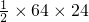 m=768m
m=768m(4)在0-24s时间内探测器上升,则上升过程的加速度为
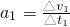 =
=
在24s后探测器开始下降,则下降过程的加速度为
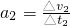 =
=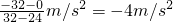
答:(1)升空后8秒末,24秒末,32秒末探测器的速度分别是64m/s,0和-32m/s.
(2)探测器8s末时刻关闭发动机,24s末时刻达到最大高度,24s末时刻开始下降.
(3)探测器所能达到的最大高度是768m.
(4)探测器加速上升的过程中加速度是8m/s2,下降过程的加速度是-4m/s2.
分析:(1)由图直接读出速度;
(2)(3)探测器先向上做匀加速运动,关闭发动机后,探测器先向上做匀减速运动,后向下做匀加速运动,由图可读出t=8s末关闭发动机.匀减速运动速度减小至零时,到达最大高度,由速度图象的“面积”大小等于位移求出最大高度.在=24s末探测器开始下落;
(4)根据速度图象的斜率等于加速度,求出加速上升和下降过程的加速度.
点评:本题通过分析探测器的运动情况,判断关闭发动机的时刻,根据“面积”大小求出最大高度,根据斜率求解加速度,都是常规问题.

练习册系列答案
相关题目
 一宇宙空间探测器从某一星球的表面垂直升空,宇宙探测器升到某一高度,发动机关闭,其速度随时间变化如图所示,
一宇宙空间探测器从某一星球的表面垂直升空,宇宙探测器升到某一高度,发动机关闭,其速度随时间变化如图所示, 一宇宙空间探测器从某一星球的表面垂直升空,宇宙探测器升空到某一高度,发动机关闭,其速度随时间的变化如图所示.宇宙探测器在该星球表面所能达到的最大高度是
一宇宙空间探测器从某一星球的表面垂直升空,宇宙探测器升空到某一高度,发动机关闭,其速度随时间的变化如图所示.宇宙探测器在该星球表面所能达到的最大高度是 一宇宙空间探测器从某一星球表面竖直升空,宇宙探测器升到空中某一高度,发动机关闭,其速度随时间的变化关系如图所示.
一宇宙空间探测器从某一星球表面竖直升空,宇宙探测器升到空中某一高度,发动机关闭,其速度随时间的变化关系如图所示. 一宇宙空间探测器从某一星球的表面竖直升空,宇宙探测器升到某一高度,发动机关闭,其速度随时间的变化关系如图所示.
一宇宙空间探测器从某一星球的表面竖直升空,宇宙探测器升到某一高度,发动机关闭,其速度随时间的变化关系如图所示. 一宇宙空间探测器从某一星球的表面竖直升空,假设探测器的质量恒为1500kg,发动机的推动力为恒力,宇宙探测器升空到某一高度时,发动机突然关闭,如图所示其速度随时间的变化规律.求
一宇宙空间探测器从某一星球的表面竖直升空,假设探测器的质量恒为1500kg,发动机的推动力为恒力,宇宙探测器升空到某一高度时,发动机突然关闭,如图所示其速度随时间的变化规律.求