��Ŀ����
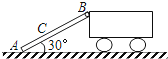
����Ŀ����ͼ��ʾ�����A��ľ��B��������Ϊm=10kg������A�Ĵ�С��B�峤L=3m����ʼʱA��B����ֹ���ָ�A��ijһˮƽ���ٶȴ�B������˿�ʼ�˶�����֪A��B��B���֮��Ķ�Ħ�������ֱ�Ϊ��1=0.3�ͦ�2=0.1��gȡ10m/s2 �� ![]()
��1�������A�պ�û�д�B�ϻ���������A�ij��ٶȶ��
��2������ľ��B���ڹ⻬ˮƽ���ϣ���A���ԣ�1���ʵij��ٶȴ�B������˿�ʼ�˶�����A�ܷ���B���룿����A��B���ٶȸ��Ƕ��
���𰸡�
��1��
�⣺A��B�������ȼ��٣����ٶȴ�Сa1=��1g=3 m/s2��
ľ��B�����ȼ��� a2= ![]() =1m/s2��
=1m/s2��
�����⣬A�պ�û�д�B�ϻ���������A����B���Ҷ�ʱ��B�ٶ���ͬ����Ϊv����
ʱ���ϵ ![]()
λ�ƹ�ϵ ![]()
��� ![]() ��m/s��
��m/s��
��2��
�⣺ľ��B���ڹ⻬���ϣ�A����B����ٶȴ�С��Ϊa1=��1g=3 m/s2��
B�����ȼ��ٵļ��ٶ� ![]() =3m/s2��
=3m/s2��
��A��B�ﵽ��ͬ�ٶ�v'ʱAû������B����ʱ���ϵ ![]()
��� ![]() m/s
m/s
A��� ![]() m
m
B��� ![]() m
m
��sA��sB=2m��֪Aû����B����
����A��B���ٶ���ȣ���СΪ ![]() m/s
m/s
����������1�������A�պ�û�д�B�ϻ��������ٽ������A����B���Ҷ�ʱ��B�ٶ���ͬ������ţ�ٵڶ����ɽ���˶�ѧ��ʽ���A�ij��ٶȣ���2������ţ�ٵڶ��������A��B�ļ��ٶȣ����A��B�ٶ����ʱ������λ�ƣ��Ӷ��ó����λ�ƣ���ľ��ij��ȱȽϣ��ж��Ƿ����룬��δ���룬���߾�����ͬ���ٶȣ�
�����㾫�������ڱ��⿼����ȱ���ֱ���˶����ٶȡ�λ�ơ�ʱ��Ĺ�ϵ����Ҫ�˽��ٶȹ�ʽ��V=V0+at��λ�ƹ�ʽ��s=v0t+1/2at2���ٶ�λ�ƹ�ʽ��vt2-v02=2as�����ϸ�ʽ��Ϊʸ��ʽ��Ӧ��ʱӦ�涨������Ȼ���ʸ����Ϊ��������⣬ͨ��ѡ���ٶȷ���Ϊ�������Ǹ�������һ�µ�ȡ��+��ֵ�����������෴��ȡ��-��ֵ���ܵó���ȷ�𰸣�