题目内容
(2009?武汉一模)如图所示,在正交坐标系xoy的第一、四象限内分别存在两个大小相等,方向不同的匀强电场,两组平行且等距的实线分别表示两个电场的电场线,每条电场线与x轴所夹的锐角为60°.一质子从y轴上某点A沿着垂直于电场线的方向射入第一象限,仅在电场力的作用下第一次到达x轴上的B点时速度方向正好垂直于第四象限内的电场线,之后第二次到达x轴上的C点.求OB与BC的比值.


分析:作出电粒子的运动的轨迹图,
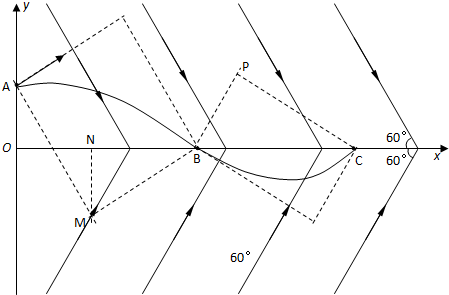
从A到B的过程:
根据几何关系:ON=AMsin30°
NB=MBcos30°
由题意知v与v0的夹角为600
沿垂直于v0方向上做匀加速运动:AM=
at12
沿平行于v0方向上做匀速直线运动:MB=v0t1
在B点:vsin60°=at1
v0=vcos60°
联立以上方程解出OB与v0的关系.
从B到C的过程:
沿CP方向做匀速直线运动:BCsin60°=vt2
沿BP方向做匀加速直线运动:BCcos60°=
at22
联立以上二式求解出BC与v0的关系.
把OB与BC相比,可得出二者之间的关系.

从A到B的过程:
根据几何关系:ON=AMsin30°
NB=MBcos30°
由题意知v与v0的夹角为600
沿垂直于v0方向上做匀加速运动:AM=
| 1 |
| 2 |
沿平行于v0方向上做匀速直线运动:MB=v0t1
在B点:vsin60°=at1
v0=vcos60°
联立以上方程解出OB与v0的关系.
从B到C的过程:
沿CP方向做匀速直线运动:BCsin60°=vt2
沿BP方向做匀加速直线运动:BCcos60°=
| 1 |
| 2 |
联立以上二式求解出BC与v0的关系.
把OB与BC相比,可得出二者之间的关系.
解答:解:电粒子的运动的轨迹如图所示,设质子在电场中运动的加速度为a,在A、B两点的速度分别为v0、v经历的时间为t1.

OB=ON+NB
由几何关系:ON=AMsin30°
NB=MBcos30°
由题意知v与v0的夹角为600
沿垂直于v0方向上:AM=
at12
沿平行于v0方向上:MB=v0t1
在B点:vsin60°=at1
v0=vcos60°
联立上述方程解得:OB=
设质子从B到C经历时间为t2作如图辅助线,
沿CP方向:BCsin60°=vt2
沿BP方向:BCcos60°=
at22
联立求解:BC=
所以:
=
答:OB与BC的比值为27:64.

OB=ON+NB
由几何关系:ON=AMsin30°
NB=MBcos30°
由题意知v与v0的夹角为600
沿垂直于v0方向上:AM=
| 1 |
| 2 |
沿平行于v0方向上:MB=v0t1
在B点:vsin60°=at1
v0=vcos60°
联立上述方程解得:OB=
| 9v02 |
| 4a |
设质子从B到C经历时间为t2作如图辅助线,
沿CP方向:BCsin60°=vt2
沿BP方向:BCcos60°=
| 1 |
| 2 |
联立求解:BC=
| 16v02 |
| 3 |
所以:
| OB |
| BC |
| 27 |
| 64 |
答:OB与BC的比值为27:64.
点评:本题关键是根据题目的意思分析粒子的运动情况,画出运动的轨迹,找出几何关系,画辅助线是解题的重要手段.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 (2009?武汉一模)如图所示,边长为L的等边三角形ABC为两有界匀强磁场的理想边界,三角形内的磁场方向垂直纸面向外,磁感应强度大小为B,三角形外的磁场(足够大)方向垂直纸面向里,磁感应强度大小也为B.把粒子源放在顶点A处,它将沿∠A的角平分线发射质量为m、电荷量为q、初速度为v0的带电粒子(粒子重力不计).若从A射出的粒子
(2009?武汉一模)如图所示,边长为L的等边三角形ABC为两有界匀强磁场的理想边界,三角形内的磁场方向垂直纸面向外,磁感应强度大小为B,三角形外的磁场(足够大)方向垂直纸面向里,磁感应强度大小也为B.把粒子源放在顶点A处,它将沿∠A的角平分线发射质量为m、电荷量为q、初速度为v0的带电粒子(粒子重力不计).若从A射出的粒子
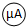 :量程0~200μA、内阻500Ω
:量程0~200μA、内阻500Ω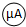 改装成一个量程略大于2.5V的伏特表,将改装表的电路图画在图甲的方框内,此伏特表
改装成一个量程略大于2.5V的伏特表,将改装表的电路图画在图甲的方框内,此伏特表 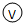 的量程是
的量程是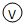 和选用的器材设计如图乙所示的电路,来测量通过小灯泡的电流强度,请在图丙的实物图上连线
和选用的器材设计如图乙所示的电路,来测量通过小灯泡的电流强度,请在图丙的实物图上连线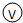 的示数为1.5V,则通过小灯泡的电流强度为
的示数为1.5V,则通过小灯泡的电流强度为 (2009?武汉一模)如图所示,一质量为m的物块A与直立的轻弹簧的上端连接,弹簧的下端固定在地面上,一质量也为m的物块叠放在A的上面,A、B处于静止状态.若A、B粘连在一起,用一竖直向上的拉力缓慢上提B,当拉力的大小为
(2009?武汉一模)如图所示,一质量为m的物块A与直立的轻弹簧的上端连接,弹簧的下端固定在地面上,一质量也为m的物块叠放在A的上面,A、B处于静止状态.若A、B粘连在一起,用一竖直向上的拉力缓慢上提B,当拉力的大小为