题目内容
总质量为80kg的跳伞运动员从悬停在离地500m的直升机上跳下,经过2s拉开绳索开启降落伞,如图13所示是跳伞过程中的v-t图,试根据图象求:(g取10m/s2)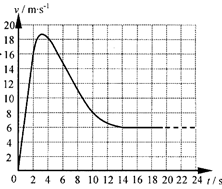
(1)t=1s时运动员的加速度和所受阻力的大小;
(2)估算14s内运动员下落的高度;
(3)估算运动员从飞机上跳下到着地面的总时间。
(1)160N;(2)约160m;(3) 71s。
解析考点:动能定理的应用;加速度;牛顿第二定律.
分析:首先分析运动员的运动情况,运动员在0-2s内做匀加速直线运动,2s-14s做变速运动,14s以后做匀速运动直到地面.t=1s时运动员做匀加速直线运动,根据图象可以算出a,根据牛顿第二定律算出f,可以通过图象与时间轴所围成的面积估算14s内运动员下落的高度,剩余的高度运动员做匀速运动,可求出匀速运动的时间,总时间即可求出.
解析:(1)在0-2S内,运动员做匀加速运动
有:a=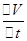 =
=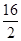 m/s2=8m/s2
m/s2=8m/s2
又:根据牛顿第二定律:mg-F=ma得
F=mg-a)=80×2N=160N
(2)速度图线与时间轴所夹面积为下落高度 h=2×2×40=160m
根据动能定理有mgh-W=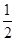 mv2
mv2
克服阻力做的功:W=mgh-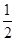 mv2=80×10×160-
mv2=80×10×160-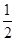 ×80×62=126560J
×80×62=126560J
(3)总时间为t=14+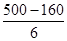 =71s
=71s
答(1)加速度为8m/s2,阻力位160N.
(2)下降高度为160m,阻力做功为126560J.
(3)着陆总时间为71s.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 (2009?惠州二模)总质量为80kg的跳伞运动员从离地500m的直升机上跳下,经过2s拉开绳索开启降落伞,如图所示是跳伞过程中的v-t图,试根据图象求:(g取10m/s2)
(2009?惠州二模)总质量为80kg的跳伞运动员从离地500m的直升机上跳下,经过2s拉开绳索开启降落伞,如图所示是跳伞过程中的v-t图,试根据图象求:(g取10m/s2)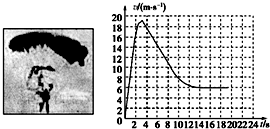 总质量为80kg的跳伞运动员从离地500m高的直升机上跳下,经过2s拉开绳索开启降落伞,如图所示是跳伞过程中的v-t图象,根据图象可知(g取10m/s2)( )
总质量为80kg的跳伞运动员从离地500m高的直升机上跳下,经过2s拉开绳索开启降落伞,如图所示是跳伞过程中的v-t图象,根据图象可知(g取10m/s2)( ) 总质量为80kg的跳伞运动员从离地500m的直升机上跳下,经过2s拉开绳索开启降落伞,如图所示是跳伞过程中的v-t图,试根据图象求:(g取10m/s2)
总质量为80kg的跳伞运动员从离地500m的直升机上跳下,经过2s拉开绳索开启降落伞,如图所示是跳伞过程中的v-t图,试根据图象求:(g取10m/s2) ?
?