题目内容
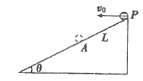
【题目】如图所示, 两个速度大小不同的同种带电粒子1、2,沿水平方向从同一点垂直射入匀强磁场中,磁场方向垂直纸面向里。当它们从磁场下边界飞出时相对入射方向的偏转角分别为90°、60°,则它们在磁场中运动的( )
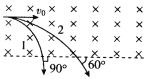
A. 轨迹半径之比为1∶2
B. 速度之比为2∶1
C. 时间之比为3∶2
D. 周期之比为2∶1
【答案】AC
【解析】
带电粒子在磁场中做匀速圆周运动,由几何关系可确定粒子的半径,根据半径公式可确定初速度;根据粒子的运动的轨迹和粒子做圆周运动的周期公式可以判断粒子的运动的时间。
A项:设粒子的入射点到磁场下边界的磁场宽度为d,画出粒子轨迹过程图,如图所示,
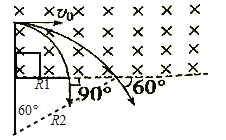
由几何关系可知:
第一个粒子的圆心为O1,由几何关系可知:R1=d;
第二个粒子的圆心为O2;由几何关系可知:R2sin30°+d=R2 ,解得:R2=2d;
故各粒子在磁场中运动的轨道半径之比为:R1:R2=1:2,故A正确;
B项:由![]() 可知v与R成正比,故速度之比也为:1:2,故B错误;
可知v与R成正比,故速度之比也为:1:2,故B错误;
C、D项:粒子在磁场中运动的周期的公式为![]() 由此可知,
由此可知,
粒子的运动的周期与粒子的速度的大小无关,所以粒子在磁场中的周期相同;
由粒子的运动的轨迹可知,三种速度的粒子的偏转角分别为90°、60°,
所以偏转角为90°的粒子的运动的时间为![]() ,偏转角为60°的粒子的运动的时间为
,偏转角为60°的粒子的运动的时间为![]() ,所以有
,所以有![]() ,故C正确,D错误。
,故C正确,D错误。
故应选:AC。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目