题目内容
将打点计时器固定在斜面上某处,一小车拖着穿过打点计时器的纸带从斜面上滑下,如图所示.
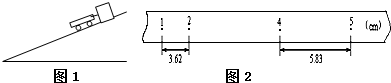
(1)如图2为接在50Hz低压交流电源上的打点计时器,在小车做匀加速直线运动时打出的一条纸带,图中所示的是每打5个点所取的记数点,但第3个记数点没有画出.由图数据可求得:该物体的加速度为
(2)为了求出小车在下滑过程中所受的阻力,除用天平测出物体质量m外,还需要用刻度尺测量的物理量有
-ma
-ma.

(1)如图2为接在50Hz低压交流电源上的打点计时器,在小车做匀加速直线运动时打出的一条纸带,图中所示的是每打5个点所取的记数点,但第3个记数点没有画出.由图数据可求得:该物体的加速度为
0.737
0.737
m/s2,第3个记数点与第2个记数点的距离约为4.36
4.36
m,打第2个记数点时该物体的速度为0.399
0.399
m/s.(以上数据结果均保留三位有效数字)(2)为了求出小车在下滑过程中所受的阻力,除用天平测出物体质量m外,还需要用刻度尺测量的物理量有
斜面上任意两点间距离L及这两点的高度差h
斜面上任意两点间距离L及这两点的高度差h
;用测得的量及加速度a表示阻力的计算式为f=| mgh |
| L |
| mgh |
| L |
分析:物体做的是匀变速直线运动,求解加速度时首先想到的应该是逐差法,但是只有两组数据,所以要找两组数据之间的关系,推论xm-xn=(m-n)at2可提供这两组数据与加速度的关系,应用这个推论即可.第2、3两点间的距离对应的应该为x2,要想得到x2必须找他和已知量的关系,x2-x1=at2提供了这个关系.
为了求出小车在下滑过程中所受的阻力,我们应该想到运用牛顿第二定律去求解.
为了求出小车在下滑过程中所受的阻力,我们应该想到运用牛顿第二定律去求解.
解答:解:(1)设1、2间的位移为x1,2、3间的位移为x2,3、4间的位移为x3,4、5间的位移为x4;
因为周期为T=0.02s,且每打5个点取一个记数点,所以每两个点之间的时间间隔T=0.1s;
由匀变速直线运动的推论xm-xn=(m-n)at2得:
x4-x1=3at2带入数据得:
(5.84-3.62)×10-2=a×0.12
解得:a=0.737m/s2.
第3个记数点与第2个记数点的距离即为x2,由匀变速直线运动的推论:x2-x1=at2得:
x2=x1+at2带入数据得:
x2=3.62×10-2+0.74×0.12=0.0436m
即为:4.36cm.
由匀变速直线运动的推论得
v2=
=0.399m/s
(2)小车在下滑过程受重力、支持力、摩擦阻力.设斜面倾角为θ
将重力分解,由牛顿第二定律得:
mgsinθ-f=ma
f=mgsinθ-ma
加速度可以运用运动学公式△x=at2求得.
为了求出小车在下滑过程中所受的阻力,已经测量小车质量,倾角直接测量很困难.我们可以测出斜面上任意两点间的距离L及这两点的高度差h,通过
=sinθ代替.
所以得:f=
-ma
故答案为:(1)0.737,4.36,0.399
(2)斜面上任意两点间距离L及这两点的高度差h,f=
-ma
因为周期为T=0.02s,且每打5个点取一个记数点,所以每两个点之间的时间间隔T=0.1s;
由匀变速直线运动的推论xm-xn=(m-n)at2得:
x4-x1=3at2带入数据得:
(5.84-3.62)×10-2=a×0.12
解得:a=0.737m/s2.
第3个记数点与第2个记数点的距离即为x2,由匀变速直线运动的推论:x2-x1=at2得:
x2=x1+at2带入数据得:
x2=3.62×10-2+0.74×0.12=0.0436m
即为:4.36cm.
由匀变速直线运动的推论得
v2=
| x13 |
| t13 |
(2)小车在下滑过程受重力、支持力、摩擦阻力.设斜面倾角为θ
将重力分解,由牛顿第二定律得:
mgsinθ-f=ma
f=mgsinθ-ma
加速度可以运用运动学公式△x=at2求得.
为了求出小车在下滑过程中所受的阻力,已经测量小车质量,倾角直接测量很困难.我们可以测出斜面上任意两点间的距离L及这两点的高度差h,通过
| h |
| L |
所以得:f=
| mgh |
| L |
故答案为:(1)0.737,4.36,0.399
(2)斜面上任意两点间距离L及这两点的高度差h,f=
| mgh |
| L |
点评:了解打点计时器的工作原理,清楚数据处理的方法.
要注意单位的换算和有效数字的保留.
要注意单位的换算和有效数字的保留.

练习册系列答案
相关题目
 (1)将打点计时器固定在斜面上某处,一小车拖着穿过打点计时器的纸带从斜面上滑下,如图所示是打出的纸带的一段.当电源频率为50Hz时,每隔0.1s取一个计数点,它们是图中a、b、c、d、e、f等点,这段时间内加速度的平均值是
(1)将打点计时器固定在斜面上某处,一小车拖着穿过打点计时器的纸带从斜面上滑下,如图所示是打出的纸带的一段.当电源频率为50Hz时,每隔0.1s取一个计数点,它们是图中a、b、c、d、e、f等点,这段时间内加速度的平均值是





 = (用被测物理量的字母表示,重力加速度为g)。与真实值相比,测量的动摩擦因数
(填“偏大”或“偏小”)。写出支持你的看法的一个论据:
。
= (用被测物理量的字母表示,重力加速度为g)。与真实值相比,测量的动摩擦因数
(填“偏大”或“偏小”)。写出支持你的看法的一个论据:
。