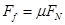题目内容
一根轻质弹簧，竖直悬挂，原长为10 cm。当弹簧下端挂2.0 N的重物时，伸长1.0 cm；则当弹簧下端挂8.0 N的重物时，弹簧长( )
| A．4.0 cm | B．14.0 cm | C．8.0 cm | D．18.0 cm |
B
解析试题分析：据题意，当弹簧下挂2N重物时，伸长1cm，据胡克定律有：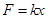
，则劲度系数为：
，则当弹簧下端挂8N物体时，弹簧伸长量为：
，所以弹簧总长为：14m。故B选项正确。
考点：本题考查胡克定律。
阅读快车系列答案关于重力、重心，下列说法正确的是（ ）
| A．任何有规则形状的物体，它的重心一定与它的几何中心重合 |
| B．用一绳子把一个物体悬挂起来，物体处于完全静止状态，该物体的重心不一定在绳子的延长线上 |
| C．任何物体的重心都在物体内，不可能在物体外 |
| D．重心与物体的形状和物体内质量分布有关 |
人们在日常生产中已经体会到，用金属制成的线材(如钢丝、钢筋)受到拉力会伸长．其实，早在17世纪英国物理学家胡克就发现，金属丝或金属杆在弹性限度内的伸长与拉力成正比，这就是著名的胡克定律．这一发现为后人对材料的研究奠定了重要基础．现有一根用新材料制成的金属杆，长为4 m，横截面积为0.8 cm2，设计要求它受到拉力后的伸长量不超过原长的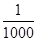
，选用同种材料制成样品进行测试，通过测试取得数据如下：
| 长度L | 拉力F伸长x横截面S | 250 N | 500 N | 750 N | 1000 N |
| 1 m | 0.05 cm2 | 0.04 cm | 0.08 cm | 0.12 cm | 0.16 cm |
| 2 m | 0.05 cm2 | 0.08 cm | 0.16 cm | 0.24 cm | 0.32 cm |
| 3 m | 0.05 cm2 | 0.12 cm | 0.24 cm | 0.36 cm | 0.46 cm |
| 4 m | 0.10 cm2 | 0.08 cm | 0.16 cm | 0.22 cm | 0.32 cm |
| 4 m | 0.20 cm2 | 0.04 cm | 0.08 cm | 0.12 cm | 0.16 cm |
(2)通过对样品的测试，求出现有金属杆在不超过设计要求伸长量前提下能承受的最大拉力．(写出过程)
(3)在表中把有明显误差的数据圈出来．
如下图（a）所示，一轻质弹簧的下端固定在水平面上，上端放置一物体(物体与弹簧不连接)，初始时物体处于静止状态．现用竖直向上的拉力F作用在物体上，使物体开始向上做匀加速运动，拉力F与物体位移s的关系如图（b）所示(g＝10 m/s2)，下列结论正确的是：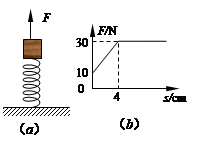 
| A．物体与弹簧分离时，弹簧处于压缩状态 |
| B．弹簧的劲度系数为750 N/m |
| C．物体的质量为2 kg |
| D．物体的加速度大小为5 m/s2 |
如图甲所示，轻质弹簧的下端固定在水平面上，上端放置一小物体(物体与弹簧不连接)，初始时物体处于静止状态。现用竖直向上的拉力F作用在物体上，使物体开始向上做匀加速直线运动，拉力F与物体位移x的关系如图乙所示(g=10m/s2)，则下列结论正确的是( )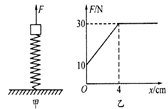
| A．物体与弹簧分离时，弹簧处于压缩状态 |
| B．物体的质量为3 kg |
| C．物体的加速度大小为5 m/s2 |
| D．弹簧的劲度系数为7. 5 N/cm |
关于弹力、摩擦力，以下说法正确的是
| A．两物体间如果存在弹力，一定同时存在摩擦力 |
| B．物体的弹性形变增大，弹力一定会随之增大 |
| C．增大两物体间的弹力，物体间的摩擦力也一定会相应增加 |
| D．同一接触面间产生的弹力和摩擦力，方向可以不垂直 |
如图所示，金属细棒质量为m，用两根相同轻弹簧吊放在水平方向的匀强磁场中，弹簧的劲度系数为k，棒ab中通有稳恒电流，棒处于平衡，并且弹簧的弹力恰好为零．若电流大小不变而方向相反，则( )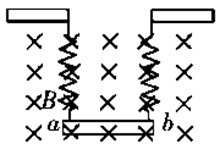
| A．每根弹簧弹力的大小为mg | B．每根弹簧弹力的大小为2mg |
| C．弹簧形变量为mg/k | D．弹簧形变量为2mg/k |
一静止于水平面上的物体，对水平面的压力FN，下列说法正确的是
| A．压力FN就是物体的重力 |
| B．压力FN是物体所受重力的平衡力 |
| C．压力FN作用在物体上 |
| D．压力FN作用在水平支持面上 |
，现用一与侧面垂直的水平力F推着B木块贴着A匀速运动，A木块依然保持静止，则A受到的摩擦力大小与B受到的摩擦力大小之比为( )
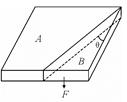
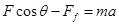
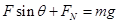D． 