Question

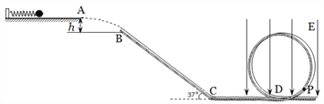
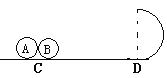
【题目】如图，质量均为1kg的小球A、B（均可视为质点）静置于水平面上的C点，D点处有一固定的竖直光滑半圆轨道，轨道半径R＝8cm，CD间距离x0=4m。现用F＝9N的水平向右的力推A，在到达D点前某时刻撤去F，此后B恰能通过半圆轨道的最高点。已知A、B与水平面动摩擦因数分别为1＝0.2，2＝0.1。求：

①力F作用的时间。

②最终A、B两球间的距离（B落地后即静止）。

Answer 1

【答案】(1)t=1s (2)x=0.09m

【解析】

①B恰能通过半圆轨道的最高点，则 ，解得v=

由最低点到最高点：，解得B在D点的速度vD=2m/s；

AB在力F作用下的加速度

撤去F后B的加速度为aB=-2g=-1m/s；

设F作用的时间为t，则

带入数据解得：t=1s 则力F作用的时间为1s.

②撤去F时AB距离D点的距离为： ，

此时AB的速度v1=a1t=3m/s；

撤去F后A的加速度为aA=-1g=-2m/s；

则A停止运动的位移

即A停止的位置距离D点0.25m；

B做平抛运动的水平位移，

则最终A、B两球间的距离0.25m-0.16m=0.09m.