题目内容
如图所示，有一倾角为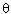
的光滑绝缘细杆，其长度为L，在细杆底端固定一带正电小球B。现将一质量为m，电荷量为q的带正电小球A套在细杆上，从最高点由静止释放，小球在到达细杆中点C时达到最大速度Vm。若重力加速度为g，静电力常量为k。求：
（1）小球B所带电荷量为多大？
（2）小球A在最高点的加速度为多少？
(3)从A到C的过程中库仑力做的功是多少？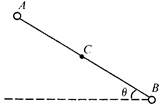
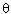的光滑绝缘细杆，其长度为L，在细杆底端固定一带正电小球B。现将一质量为m，电荷量为q的带正电小球A套在细杆上，从最高点由静止释放，小球在到达细杆中点C时达到最大速度Vm。若重力加速度为g，静电力常量为k。求：（1）小球B所带电荷量为多大？
（2）小球A在最高点的加速度为多少？
(3)从A到C的过程中库仑力做的功是多少？
（1）
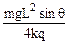（2）a=
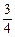g sinq（3）W库=
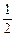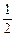mVm2-mgLsinq(1)因为小球在C点达到最大速度
所以小球在C处所受合力为零，设B带电量为QB
即F库=mg·sinq ① ……………………(1分)
由库仑定律得F库=k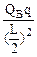
②……………………(1分)
由①②得：QB=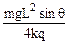……………………(2分)
(2)在最高点对小球作受力分析，由牛顿第二定律得：
F合=mgsinq-F'库="ma" ③……………………(1分)
F'库=k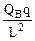
=
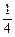mgsinq④ ……………………(1分)
由③④得：a=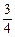g sinq…………………………(2分)
(3)从A到C由动能定理得：
mg·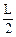
·sinq+W库=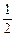mVm2-0
\W库=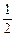mVm2-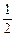mgLsinq……………………(6分)
所以小球在C处所受合力为零，设B带电量为QB
即F库=mg·sinq ① ……………………(1分)
由库仑定律得F库=k
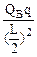②……………………(1分)由①②得：QB=
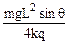……………………(2分)(2)在最高点对小球作受力分析，由牛顿第二定律得：
F合=mgsinq-F'库="ma" ③……………………(1分)
F'库=k
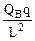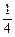=mgsinq④ ……………………(1分)由③④得：a=
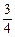g sinq…………………………(2分)(3)从A到C由动能定理得：
mg·
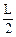·sinq+W库=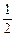mVm2-0 \W库=
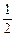mVm2-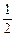mgLsinq……………………(6分)
练习册系列答案
相关题目
B.
C.3 D. 
，
