题目内容
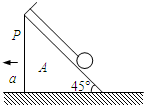 如图所示,细线的一端固定于倾角为45°的光滑楔形滑块A的顶端P处,细线的另一端拴一质量为m的小球,当滑块至少以加速度a=
如图所示,细线的一端固定于倾角为45°的光滑楔形滑块A的顶端P处,细线的另一端拴一质量为m的小球,当滑块至少以加速度a=分析:小球对滑块的压力等于零,对木块进行受力分析,其受到重力和绳子的拉力,合力水平向左,再根据牛顿第二定律就可以求得加速度;,当滑块以a=2g的加速度向左运动时,小球将离开滑块,绳子张力变得更大,其受到重力和绳子的拉力,合力水平向左,求绳子的拉力
解答:解:(1)对物体进行受力分析,如图所示:
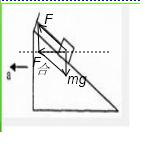
由图知,F合=mg
故a=g
(2)由上图得,当a=2g时,
F合=ma=2mg
由勾股定理得:
F=
=
mg
答案为:g、
mg

由图知,F合=mg
故a=g
(2)由上图得,当a=2g时,
F合=ma=2mg
由勾股定理得:
F=
(mg)2
|
| 5 |
答案为:g、
| 5 |
点评:该题是牛顿第二定律的直接应用,解题的关键是正确对物体进行受力分析求出合力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
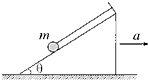 如图所示,细线的一端系一质量为m的小球,另一端固定在倾角为θ的光滑斜面体顶端,细线与斜面平行.在斜面体以加速度a水平向右做匀加速直线运动的过程中,小球始终静止在斜面上,重力加速度为g,小球受到细线的拉力为T,斜面的支持力为FN,则( )
如图所示,细线的一端系一质量为m的小球,另一端固定在倾角为θ的光滑斜面体顶端,细线与斜面平行.在斜面体以加速度a水平向右做匀加速直线运动的过程中,小球始终静止在斜面上,重力加速度为g,小球受到细线的拉力为T,斜面的支持力为FN,则( )| A、T=m(g sinθ+a cosθ) | B、T=m(g cosθ+a sinθ) | C、FN=m(g cosθ-a sinθ) | D、FN=m(g cosθ+a sinθ) |
 如图所示,细线的一端固定于倾角为45°的光滑楔形滑块A的顶端P处,细线的另一端拴一质量为m的小球.当细线对小球的拉力刚好等于零时,水平向右的加速度a的大小为(g为重力加速度)( )
如图所示,细线的一端固定于倾角为45°的光滑楔形滑块A的顶端P处,细线的另一端拴一质量为m的小球.当细线对小球的拉力刚好等于零时,水平向右的加速度a的大小为(g为重力加速度)( ) (2013?琼海模拟)如图所示,细线的一端固定于O点,另一端系一小球.在水平拉力F作用下,小球以恒定速率在竖直平面内由A点运动到B点.在此过程中下列说法正确的是( )
(2013?琼海模拟)如图所示,细线的一端固定于O点,另一端系一小球.在水平拉力F作用下,小球以恒定速率在竖直平面内由A点运动到B点.在此过程中下列说法正确的是( ) (2013?静安区二模)如图所示,细线的一端固定于O点,另一端系一小球,在水平拉力F作用下,小球以恒定速率在竖直平面内由A点运动到B点的过程中( )
(2013?静安区二模)如图所示,细线的一端固定于O点,另一端系一小球,在水平拉力F作用下,小球以恒定速率在竖直平面内由A点运动到B点的过程中( )