题目内容
【题目】如图所示,在E = 103 V/m的水平向左匀强电场中,有一光滑半圆形绝缘轨道竖直放置,轨道与一水平绝缘轨道MN连接,半圆轨道所在竖直平面与电场线平行,其半径R =0.4 m,一带正电荷q=10-4 C的小滑块质量为m= 0.04 kg,与水平轨道间的动摩擦因数μ=0.2,g取10 m/s2,求:
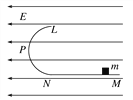
(1)要使小滑块能运动到半圆轨道的最高点L,滑块应在水平轨道上离N点多远处释放?
(2)这样释放的滑块通过P点时对轨道的压力是多大?(P为半圆轨道中点)
【答案】(1)20 m (2)1.5 N
【解析】(1)设滑块与N点的距离为L,分析滑块的运动过程,由动能定理可得,
qEL-μmgL-mg2R=![]() mv2-0
mv2-0
小滑块在D点时,重力提供向心力,所以 mg=m![]()
代入数据解得 v=2m/s,L=20m.
(2)滑块到达P点时,对全过程应用动能定理可得,
qE(L+R)-μmgL-mgR=![]() mvP2-0
mvP2-0
在P点时由牛顿第二定律可得,N-qE=m![]()
解得N=1.5N
由牛顿第三定律可得,滑块通过P点时对轨道压力是1.5N.

【题目】某同学在探究弹力和弹簧伸长的关系,并测定弹簧的劲度系数k。
主要实验步骤如下:将待测弹簧的一端固定在铁架台上,然后将毫米刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好指在刻度尺上。当弹簧自然下垂时,指针的指示值记作L0;弹簧下端挂一个砝码时,指针的指示值记作L1;弹簧下端挂两个砝码时,指针的指示值记作L2 ……;挂七个砝码时,指针的位置如图所示,指针的指示值记作L7。已知每个砝码的质量均为50 g,测量记录表:

代表符号 | L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
刻度数值/cm | 1.70 | 3.40 | 5.10 | 6.85 | 8.60 | 10.30 | 12.10 |
(1)实验中,L7的值还未读出,请你根据上图将这个测量值填入记录表中。
(2)为充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了四个差值:d1=L4–L0,d2=L5–L1,d3=L6–L2,d4=L7–L3。
(3)根据以上差值,可以求出每增加50 g砝码的弹簧平均伸长量ΔL。ΔL用d1、d2、d3、d4表示的式子为ΔL=_________________。
(4)计算弹簧的劲度系数k=________N/m。(g取9.8 m/s2)