Question

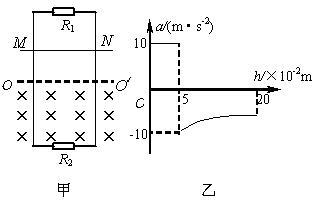如图甲所示，平行金属导轨竖直放置，导轨间距为L=1m，上端接有定值电阻R₁＝3Ω，下端接有电阻R₂＝6Ω，虚线OOˊ下方是垂直于导轨平面的匀强磁场。现将质量m=0.1kg、电阻不计的金属杆MN从OOˊ上方某处垂直导轨放置后由静止释放，杆下落0.2m过程中加速度a与下落距离h的关系图象如图乙所示(金属杆运动过程中始终与导轨保持良好接触)。求：

（1）磁感应强度B；

（2）杆下落0.2m过程中通过电阻R₂的电荷量q；

Answer 1

（1）B＝2T；（2）q=0.05C。

解析:

（1）由图象知，杆自由下落距离是0.05m，当地重力加速度g=10m/s²，则杆进入磁场时的速度v==1m/s

由图象知，杆进入磁场时加速度a=－g＝－10 m/s²，由牛顿第二定律得

mg－F_安＝ma

回路中的电动势E＝BLv

杆中的电流I＝

R_并＝

F_安＝BIL=

得B＝＝2T

（2）杆在磁场中运动产生的平均感应电动势

杆中的平均电流

通过杆的电荷量

Q＝

q=Q=0.05C

本题意在以金属导体在磁场中做切割磁感线运动为背景，考查电磁感应、恒定电流、力学规律等知识的综合应用，同时考查从物理图象中获取信息的能力，需要考生把金属杆下落0.2m过程中加速度a～h的关系图象所反映的物理过程清晰的展现出来。