题目内容
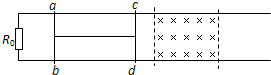 如图所示,在足够长的两条平行金属导轨的左端接有一个定值电阻R0,两导轨间的距离L=0.5m,在虚线的区域内有与导轨平面垂直的匀强磁场,磁感应强度B=0.2T,虚线间的距离S=1.0m.完全相同的金属棒ab、cd与导轨垂直放置,两棒间用2.0m长的绝缘轻杆连接.棒与导轨间无摩擦,两棒电阻皆为r=0.3Ω,导轨电阻不计.已知R0=2r.现用一外力从图示位置水平向右拉cd棒,使两棒以v=5.0m/s的速度向右匀速穿过磁场区域.求:
如图所示,在足够长的两条平行金属导轨的左端接有一个定值电阻R0,两导轨间的距离L=0.5m,在虚线的区域内有与导轨平面垂直的匀强磁场,磁感应强度B=0.2T,虚线间的距离S=1.0m.完全相同的金属棒ab、cd与导轨垂直放置,两棒间用2.0m长的绝缘轻杆连接.棒与导轨间无摩擦,两棒电阻皆为r=0.3Ω,导轨电阻不计.已知R0=2r.现用一外力从图示位置水平向右拉cd棒,使两棒以v=5.0m/s的速度向右匀速穿过磁场区域.求:(1)从cd棒刚进磁场到ab棒刚离开磁场的过程中通过ab棒的电流大小和方向;
(2)从cd棒刚进磁场到ab棒刚离开磁场的过程中拉力做的功;
(3)若cd棒刚进入磁场时将水平外力去掉,经一段时间cd棒出磁场,求此段时间内通过cd 棒的电量.
分析:(1)根据切割产生的感应电动势公式求出电动势的大小,结合闭合电路欧姆定律求出感应电流的大小,通过右手定则判断感应电流的方向.
(2)从cd棒刚进磁场到ab棒刚离开磁场的过程中拉力做的功等于电路中消耗的电能,结合能量守恒定律求出拉力做功的大小.
(3)结合法拉第电磁感应定律和电量的公式求出这段时间内通过cd棒的电量.
(2)从cd棒刚进磁场到ab棒刚离开磁场的过程中拉力做的功等于电路中消耗的电能,结合能量守恒定律求出拉力做功的大小.
(3)结合法拉第电磁感应定律和电量的公式求出这段时间内通过cd棒的电量.
解答:解:(1)cd棒进入磁场到ab棒离开磁场的过程中,回路外电阻R=
=
r=0.2Ω
感应电动势的大小E=BLv=0.2×0.5×5=0.5V
根据闭合电路欧姆定律得,I=
=1.0A
当cd边在磁场中时Iab=
=
=0.67A 方向a→b
当ab边进入磁场时 Iab=I=1.0A 方向b→a
(2)两棒以v=5.0m/s的速度向右匀速穿过磁场区域的时间t=
s=0.4s.
拉力做的功等于电路消耗的电能
W=Q=I2(R+r)t=1×0.5×0.4J=0.2 J
(3)根据法拉第电磁感应定律得,E=
=
则通过的电量q=
△t=
=
C=0.2C
答:(1)当cd边在磁场中时,电流的大小为0.67A,方向a→b;当ab边进入磁场时,电流的大小为1.0A,方向b→a.
(2)从cd棒刚进磁场到ab棒刚离开磁场的过程中拉力做的功为0.2J.
(3)此段时间内通过cd 棒的电量为0.2C.
| 2r?r |
| 2r+r |
| 2 |
| 3 |
感应电动势的大小E=BLv=0.2×0.5×5=0.5V
根据闭合电路欧姆定律得,I=
| E |
| R+r |
当cd边在磁场中时Iab=
| IR |
| r |
| 0.1×0.2 |
| 0.3 |
当ab边进入磁场时 Iab=I=1.0A 方向b→a
(2)两棒以v=5.0m/s的速度向右匀速穿过磁场区域的时间t=
| 2 |
| 5 |
拉力做的功等于电路消耗的电能
W=Q=I2(R+r)t=1×0.5×0.4J=0.2 J
(3)根据法拉第电磁感应定律得,E=
| △Φ |
| △t |
| BLS |
| △t |
则通过的电量q=
. |
| I |
| BLS |
| R总 |
| 0.2×0.5×1 |
| 0.5 |
答:(1)当cd边在磁场中时,电流的大小为0.67A,方向a→b;当ab边进入磁场时,电流的大小为1.0A,方向b→a.
(2)从cd棒刚进磁场到ab棒刚离开磁场的过程中拉力做的功为0.2J.
(3)此段时间内通过cd 棒的电量为0.2C.
点评:本题考查了电磁感应与电路和能量的综合,是高考的常见题型,难度中等,需加强这方面的训练.

练习册系列答案
相关题目
 如图所示,在足够长的粗糙水平桌面上,静止放置质量为m1=0.20
如图所示,在足够长的粗糙水平桌面上,静止放置质量为m1=0.20 如图所示,在足够长的光滑水平轨道上静止三个小木块A、B、C,质量分别为mA=1kg,mB=1kg,mC=2kg,其中B与C用一个轻弹簧固定连接,开始时整个装置处于静止状态;A和B之间有少许塑胶炸药,A的左边有一个弹性挡板(小木块和弹性挡板碰撞过程没有能量损失).现在引爆塑胶炸药,若炸药爆炸产生的能量有E=9J转化为A和B沿轨道方向的动能,A和B分开后,A恰好在B、C之间的弹簧第一次恢复到原长时追上B,并且与B发生碰撞后粘在一起.求:
如图所示,在足够长的光滑水平轨道上静止三个小木块A、B、C,质量分别为mA=1kg,mB=1kg,mC=2kg,其中B与C用一个轻弹簧固定连接,开始时整个装置处于静止状态;A和B之间有少许塑胶炸药,A的左边有一个弹性挡板(小木块和弹性挡板碰撞过程没有能量损失).现在引爆塑胶炸药,若炸药爆炸产生的能量有E=9J转化为A和B沿轨道方向的动能,A和B分开后,A恰好在B、C之间的弹簧第一次恢复到原长时追上B,并且与B发生碰撞后粘在一起.求: 如图所示,在足够长的光滑绝缘水平直线轨道上方h高度的P点,固定一电荷量为+Q的点电荷.一质量为m、带电荷量为+q的物块(可视为质点),从轨道上的A点以初速度v0沿轨道向右运动,当运动到P点正下方B点时速度为v.已知点电荷产生的电场在A点的电势为φ(取无穷远处电势为零),PA连线与水平轨道的夹角为60°,试求:
如图所示,在足够长的光滑绝缘水平直线轨道上方h高度的P点,固定一电荷量为+Q的点电荷.一质量为m、带电荷量为+q的物块(可视为质点),从轨道上的A点以初速度v0沿轨道向右运动,当运动到P点正下方B点时速度为v.已知点电荷产生的电场在A点的电势为φ(取无穷远处电势为零),PA连线与水平轨道的夹角为60°,试求: (2011?海淀区模拟)如图所示,在足够长的光滑水平轨道上有三个小木块A、B、C,质量分别为mA、mB、mC,且mA=mB=1.0kg,mC=2.0kg,其中B与C用一个轻弹簧拴接在一起,开始时整个装置处于静止状态.A和B之间有少许塑胶炸药,A的左边有一个弹性挡板.现在引爆塑胶炸药,若炸药爆炸产生的能量中有E=9.0J转化为A和B的动能,A和B分开后,A恰好在B、C之间的弹簧第一次恢复到原长时追上B,并且与B发生碰撞后粘在一起.忽略小木块和弹性挡板碰撞过程中的能量损失.求:
(2011?海淀区模拟)如图所示,在足够长的光滑水平轨道上有三个小木块A、B、C,质量分别为mA、mB、mC,且mA=mB=1.0kg,mC=2.0kg,其中B与C用一个轻弹簧拴接在一起,开始时整个装置处于静止状态.A和B之间有少许塑胶炸药,A的左边有一个弹性挡板.现在引爆塑胶炸药,若炸药爆炸产生的能量中有E=9.0J转化为A和B的动能,A和B分开后,A恰好在B、C之间的弹簧第一次恢复到原长时追上B,并且与B发生碰撞后粘在一起.忽略小木块和弹性挡板碰撞过程中的能量损失.求: