题目内容
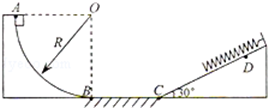
1.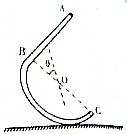 如图所示,水平地面上固定一个内壁光滑的“J”形管ABC,“J”形管在竖直平面内,BC部分是一个半径为R的半圆管道,AB部分是一个长度为2R的直管道,直管道AB垂直于半圆管道的直径BC,直径BC与竖直方向的夹角为θ(0°<θ≤90°),将一可视为质点的小球从A端由静止沿管道释放,重力加速度为g,求:
如图所示,水平地面上固定一个内壁光滑的“J”形管ABC,“J”形管在竖直平面内,BC部分是一个半径为R的半圆管道,AB部分是一个长度为2R的直管道,直管道AB垂直于半圆管道的直径BC,直径BC与竖直方向的夹角为θ(0°<θ≤90°),将一可视为质点的小球从A端由静止沿管道释放,重力加速度为g,求:(1)当θ取多大角度时,小球在直管道中运动的时间最短,最短时间为多少?
(2)当θ取多大角度时,小球到达C端速度最大,最大速度为多少?
分析 (1)小球从A运动到B做匀加速直线运动,根据牛顿第二定律求出加速度,再根据位移时间公式求出时间的表达式即可;
(2)先根据几何关系求出A到C的高度差,从A到C的过程中,根据动能定理列式求出C点的速度表达式,再根据数学知识求解最大值.
解答 解:(1)小球从A运动到B做匀加速直线运动,根据牛顿第二定律得:
a=$\frac{mgsinθ}{m}$=gsinθ
根据2R=$\frac{1}{2}a{t}^{2}$得:
t=$\sqrt{\frac{4R}{gsinθ}}$,
当θ=90°时,t最短,最短时间为:${t}_{min}=\sqrt{\frac{4R}{g}}$,
(2)根据几何关系可知,A到C的高度差为:h=2Rsinθ+2Rcosθ,
从A到C的过程中,根据动能定理得:$\frac{1}{2}m{v}^{2}=mg(2Rsinθ+2Rcosθ)$
解得:v=$\sqrt{4gR(sinθ+cosθ)}$=$\sqrt{2\sqrt{2}gRsin(θ+45°)}$,
当θ=45°时,v最大,最大为${v}_{m}=\sqrt{2\sqrt{2}gR}$.
答:(1)当θ取90°角度时,小球在直管道中运动的时间最短,最短时间为$\sqrt{\frac{4R}{g}}$;
(2)当θ取45°角度时,小球到达C端速度最大,最大速度为$\sqrt{2\sqrt{2}gR}$.
点评 本题主要考查了牛顿第二定律、运动学基本公式以及动能定理的直接应用,解题时注意数学知识的应用,难度适中.

练习册系列答案
相关题目
17.下列关于质点的说法中,正确的是( )
| A. | 质点就是质量很小的物体 | |
| B. | 质点就是体积很小的物体 | |
| C. | 质点是一种理想化模型,实际上并不存在 | |
| D. | 花样滑冰运动员在比赛中,可以视为质点 |
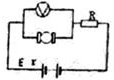 如图所示电路,电动机的线圈电阻是1Ω,电动机工作时电压表的示数是12V,电池组的电动势是22V,内电阻是1Ω,电阻R的阻值为4Ω.不考虑电压表对电路的影响.求:
如图所示电路,电动机的线圈电阻是1Ω,电动机工作时电压表的示数是12V,电池组的电动势是22V,内电阻是1Ω,电阻R的阻值为4Ω.不考虑电压表对电路的影响.求: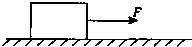 如图所示,用F=2.0N的水平拉力,使质量m=2.0kg的物体由静止开始沿光滑水平面做匀加速直线运动.求:
如图所示,用F=2.0N的水平拉力,使质量m=2.0kg的物体由静止开始沿光滑水平面做匀加速直线运动.求: 图中AOB是一内表面光滑的楔形槽,固定在水平桌面(图中纸面)上,夹角α=1°(为了能看清楚,图中画的是夸大了的).现将一质点在BOA面内从A处以速度v=5m/s射出,其方向与AO间的夹角θ=60°,OA=10m.设质点与桌面间的摩擦可忽略不计,质点与OB面及OA面的碰撞都是弹性碰撞,且每次碰撞时间极短,可忽略不计,试求:
图中AOB是一内表面光滑的楔形槽,固定在水平桌面(图中纸面)上,夹角α=1°(为了能看清楚,图中画的是夸大了的).现将一质点在BOA面内从A处以速度v=5m/s射出,其方向与AO间的夹角θ=60°,OA=10m.设质点与桌面间的摩擦可忽略不计,质点与OB面及OA面的碰撞都是弹性碰撞,且每次碰撞时间极短,可忽略不计,试求: 如图所示,在粗糙水平面上相距L=1.0m处,固定有两个绝缘挡板M,N,在它们正中间有一个质量为m=5.0×10-2kg,电荷量为q=-2.0×10-4C的带电物体A(可视为质点),A与水平面间的动摩擦因数μ=0.10,空间有水平向右的匀强电场,场强E=2.5×102V/m.取g=10m/s2,现给A一个初速度v0=3.0m/s向右运动,设A与挡板M,N碰撞过程没有动能损失.求:
如图所示,在粗糙水平面上相距L=1.0m处,固定有两个绝缘挡板M,N,在它们正中间有一个质量为m=5.0×10-2kg,电荷量为q=-2.0×10-4C的带电物体A(可视为质点),A与水平面间的动摩擦因数μ=0.10,空间有水平向右的匀强电场,场强E=2.5×102V/m.取g=10m/s2,现给A一个初速度v0=3.0m/s向右运动,设A与挡板M,N碰撞过程没有动能损失.求: 如图所示,一个质量为M的长圆管竖直放置,顶端塞有一个质量为m的弹性小球,M=4m,球和管间的滑动摩擦力和最大静摩擦力大小均为4mg,管从下端离地面距离为H处自由落下,运动过程中,管始终保持竖直,每次落地后向上弹起的速度与落地时速度大小相等,不计空气阻力,重力加速度为g.求:
如图所示,一个质量为M的长圆管竖直放置,顶端塞有一个质量为m的弹性小球,M=4m,球和管间的滑动摩擦力和最大静摩擦力大小均为4mg,管从下端离地面距离为H处自由落下,运动过程中,管始终保持竖直,每次落地后向上弹起的速度与落地时速度大小相等,不计空气阻力,重力加速度为g.求: 火箭内的实验平台有质量为18㎏的测试仪器,火箭从地面起动后以加速度a=$\frac{g}{2}$竖直匀加速上升,g=10m/s2试求:
火箭内的实验平台有质量为18㎏的测试仪器,火箭从地面起动后以加速度a=$\frac{g}{2}$竖直匀加速上升,g=10m/s2试求: