题目内容
11.如图所示,水平轨道BC的左端与固定的光滑竖直$\frac{1}{4}$圆轨道相切与B点,右端与一倾角为30°的光滑斜面轨道在C点平滑连接(即物体经过C点时速度的大小不变),斜面顶端固定一轻质弹簧,一质量为2kg的滑块从圆弧轨道的顶端A点由静止释放,经水平轨道后滑上斜面并压缩弹簧,第一次可将弹簧压缩至D点,已知光滑圆轨道的半径R=0.45m,水平轨道BC长为0.4m,其动摩擦因数μ=0.2,光滑斜面轨道上CD长为0.6m,g取10m/s2,求: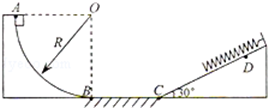
(1)滑块第一次经过B点时对轨道的压力
(2)整个过程中弹簧具有最大的弹性势能;
(3)滑块在BC上通过的总路程.
分析 (1)由A到B过程由动能定理可求得B点的速度,再由向心力公式可求得B点的作用力;
(2)对AD过程由动能定理可求得弹簧的弹性势能;
(3)对滑块运动的整个过程,由动能定理列式,可求得在BC上通过的总路程.
解答 解:(1)滑块从A点到B点,由动能定理可得:
mgR=$\frac{1}{2}m{v}_{B}^{2}$-0,
代入数据解得:vB=3m/s
滑块在B点,由牛顿第二定律得:
F-mg=m$\frac{{v}_{B}^{2}}{R}$,
代入数据解得:F=3mg=60N
由牛顿第三定律可得:物块对B点的压力:F′=F=60N;
(2)滑块从A点到D点,该过程弹簧弹力对滑块做的功为W,由动能定理可得:
mgR-μmgLBC-mgLCDsin30°+W=0,
其中:EP=-W,
代入数据解得:EP=1.4J;
即整个过程中弹簧具有最大的弹性势能为1.4J.
(3)滑块最终停止在水平轨道BC间,设滑块在BC上通过的总路程为s.从滑块第一次经过B点到最终停下来的全过程,由动能定理可得:
-μmgs=0-$\frac{1}{2}m{v}_{B}^{2}$,
代入数据解得:s=2.25m
答:(1)滑块第一次经过B点时对轨道的压力大小为60N,方向:竖直向下;
(2)整个过程中弹簧具有最大的弹性势能为1.4J;
(3)滑块在BC上通过的总路程是2.25m.
点评 本题考查动能定理及牛顿第二定律等内容,要注意正确受力分析;对于不涉及时间的问题,可优先选用动能定理.

练习册系列答案
相关题目
19.如图所示的xOy坐标系中,x轴上固定一个点电荷Q,y轴上固定一根光滑绝缘细杆(细杆的下端刚好在坐标原点O处),将一个套在杆上重力不计的带电圆环(视为质点)从杆上P处由静止释放,圆环从O处离开细杆后恰好绕点电荷Q做圆周运动.下列说法正确的是( )


| A. | 圆环沿细杆从P运动到O的过程中,速度可能先增大后减小 | |
| B. | 圆环沿细杆从P运动到O的过程中,加速度可能先增大后减小 | |
| C. | 无论增大圆环所带的电荷量或增大点电荷Q的电荷量,其他条件不变,圆环离开细杆后仍然能绕点电荷做圆周运动 | |
| D. | 将圆环从杆上P的上方由静止释放,其他条件不变,圆环离开细杆后仍然能绕点电荷做圆周运动 |
16. 科学家在实验室中找到一种材料,它的I-U曲线如图,OC段为曲线,CD段为直线,CD的连线与横轴的交点在原点的左侧,下列说法正确的是( )
科学家在实验室中找到一种材料,它的I-U曲线如图,OC段为曲线,CD段为直线,CD的连线与横轴的交点在原点的左侧,下列说法正确的是( )
 科学家在实验室中找到一种材料,它的I-U曲线如图,OC段为曲线,CD段为直线,CD的连线与横轴的交点在原点的左侧,下列说法正确的是( )
科学家在实验室中找到一种材料,它的I-U曲线如图,OC段为曲线,CD段为直线,CD的连线与横轴的交点在原点的左侧,下列说法正确的是( )| A. | 该材料的电阻随电流的增大而一直增大 | |
| B. | 该材料的电阻随电流的先增大后不变 | |
| C. | 该材料的电阻随电流的增大而一直减小 | |
| D. | 该材料的电阻随电流的先减小后不变 |
1.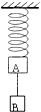 如图所示,轻质弹簧下挂重为400N的物体A,伸长了4cm,再挂上重为200N的物体B时又伸长了2cm,弹簧均在弹性限度内.若将连接A、B两物体的细绳烧断,则烧断细绳的瞬间,A、B两物体的加速度大小分别为(g=10m/s2)( )
如图所示,轻质弹簧下挂重为400N的物体A,伸长了4cm,再挂上重为200N的物体B时又伸长了2cm,弹簧均在弹性限度内.若将连接A、B两物体的细绳烧断,则烧断细绳的瞬间,A、B两物体的加速度大小分别为(g=10m/s2)( )
 如图所示,轻质弹簧下挂重为400N的物体A,伸长了4cm,再挂上重为200N的物体B时又伸长了2cm,弹簧均在弹性限度内.若将连接A、B两物体的细绳烧断,则烧断细绳的瞬间,A、B两物体的加速度大小分别为(g=10m/s2)( )
如图所示,轻质弹簧下挂重为400N的物体A,伸长了4cm,再挂上重为200N的物体B时又伸长了2cm,弹簧均在弹性限度内.若将连接A、B两物体的细绳烧断,则烧断细绳的瞬间,A、B两物体的加速度大小分别为(g=10m/s2)( )| A. | aA=0 aB=10m/s2 | B. | aA=10m/s2 aB=0 | ||
| C. | aA=5m/s2 aB=10m/s2 | D. | aA=10m/s2 aB=5m/s2 |
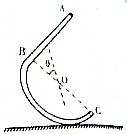 如图所示,水平地面上固定一个内壁光滑的“J”形管ABC,“J”形管在竖直平面内,BC部分是一个半径为R的半圆管道,AB部分是一个长度为2R的直管道,直管道AB垂直于半圆管道的直径BC,直径BC与竖直方向的夹角为θ(0°<θ≤90°),将一可视为质点的小球从A端由静止沿管道释放,重力加速度为g,求:
如图所示,水平地面上固定一个内壁光滑的“J”形管ABC,“J”形管在竖直平面内,BC部分是一个半径为R的半圆管道,AB部分是一个长度为2R的直管道,直管道AB垂直于半圆管道的直径BC,直径BC与竖直方向的夹角为θ(0°<θ≤90°),将一可视为质点的小球从A端由静止沿管道释放,重力加速度为g,求: 如图所示,质量为m的光滑小球,用轻绳连接后,挂在三角劈的顶端,绳与斜面平行,三角劈可以在水平方向上左右运动,求:
如图所示,质量为m的光滑小球,用轻绳连接后,挂在三角劈的顶端,绳与斜面平行,三角劈可以在水平方向上左右运动,求: 足够长光滑斜面BC的倾角α=37°,小物块与水平面间的动摩擦因数为0.5,水平面与斜面之间B点有一小段弧形连接,一质量m=2kg的小物块静止于A点,现在AB段对小物块施加与水平方向成α=37°向上的恒力F作用,如图所示,已知AB间的距离为16m,且物体从A点运动到B点所用时间t=8s,当物体到达B点时迅速撤去恒力F(已知sin37°=0.6,cos37°=0.8,g=10m/s2).求:
足够长光滑斜面BC的倾角α=37°,小物块与水平面间的动摩擦因数为0.5,水平面与斜面之间B点有一小段弧形连接,一质量m=2kg的小物块静止于A点,现在AB段对小物块施加与水平方向成α=37°向上的恒力F作用,如图所示,已知AB间的距离为16m,且物体从A点运动到B点所用时间t=8s,当物体到达B点时迅速撤去恒力F(已知sin37°=0.6,cos37°=0.8,g=10m/s2).求:
 具有完全自主产权的我国深海探测器“探索”号能够载人下潜超七千米,再创载人深潜新纪录.在某次深潜实验中,“探索”号探测到390m深处的海水温度为280K.某同学利用该数据来研究气体状态随海水温度的变化,如图所示,导热性良好的气缸内封闭一定质量的气体,不计活塞的质量和摩擦,气缸所处海平面的温度To=300K,压强P0=1atm,封闭气体的体积Vo=3m2.如果将该气缸下潜至390m深处,此过程中封闭气体可视为理想气体.求:390m深处封闭气体的体积(1atm相当于10m深的海水产生的压强).
具有完全自主产权的我国深海探测器“探索”号能够载人下潜超七千米,再创载人深潜新纪录.在某次深潜实验中,“探索”号探测到390m深处的海水温度为280K.某同学利用该数据来研究气体状态随海水温度的变化,如图所示,导热性良好的气缸内封闭一定质量的气体,不计活塞的质量和摩擦,气缸所处海平面的温度To=300K,压强P0=1atm,封闭气体的体积Vo=3m2.如果将该气缸下潜至390m深处,此过程中封闭气体可视为理想气体.求:390m深处封闭气体的体积(1atm相当于10m深的海水产生的压强).