Question

【题目】如图所示，空间有一垂直纸面向外，磁感应强度为0.5T的匀强磁场，一质量为0.2lg且足够长的绝缘木板静止在光滑水平面上，，在木板的左端无初速放置一质量为0.1kg，电荷量q=+0.2C的滑块，滑块与绝缘木板之间动摩擦因数为0.5，滑块受到的最大静摩擦力可认为等于滑动摩擦力．t=0时对木板施加方向水平向左，大小为0.6N的恒力F，g取10m/s2．则

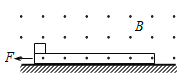
A. 木板和滑块一直做加速度为2m/s2的匀加速运动

B. 滑块开始做加速度减小的变加速运动，最后做速度为10m/s匀速运动

C. 木板先做加速度为2m/s2匀加速运动，再做加速度增大的运动，最后做加速度为3m/s2的匀加速运动

D. 开始木板和滑块一起做加速度为2m/s2的匀加速运动，5s末滑块开始做匀速运动，木板做加速度为3m/s2的匀加速运动

Answer 1

【答案】C

【解析】由于动摩擦因数为0.5，静摩擦力能提供的最大加速度：a0=μg=0.5×10=5m/s2，当0.6N的恒力作用于木板时，系统一起以=2m/s2＜5m/s2的加速度一起运动；当滑块获得向左运动的速度以后又产生一个方向向上的洛伦兹力：f=qvB，当滑块速度为v时，两者开始相对于滑动，由牛顿第二定律得，对滑块：μ（mg-qvB）=ma′，对木板：F-μ（mg-qvB）=Ma′，解得：v=4.5m/s，当滑块的速度为4.5m/s滑块相对于木板滑动，滑块向左做加速运动，洛伦兹力f=qvB，由于v变大，洛伦兹力变大，滑动摩擦力：μ（mg-qvB）变小，滑块的加速度变小，滑块做加速度减小的加速运动，在此过程中，由于滑动摩擦力减小，木板受到的合力变大，木板做加速度增大的加速运动；当洛伦兹力等于重力时滑块与木板之间的弹力为零，此时：Bqv′=mg，解得：v′=10m/s，此时摩擦力消失，滑块做匀速运动，而木板在恒力作用下做匀加速运动： =3m/s2；由以上分析可知：开始木板与木块一起做匀加速直线运动，加速度为2m/s2；当木板与木块的速度达到4.5m/s后，滑块做加速度减小的加速运动，木板做加速度增大的加速运动；当滑块的速度为10m/s时后，滑块做匀速直线运动，木板做匀加速直线运动，木板的加速度为3m/s2；故AB错误，C正确．如果滑块一直以2m/s2的加速度做匀加速直线运动，则经过5s滑块的速度达到10m/s，由A的分析可知，滑块先以2m/s2的加速度做匀加速直线运动，然后做加速度减小的加速运动，最后速度达到10m/s，由此可知，滑块速度达到10m/s需要的时间大于5s，由此可知，木板在5s以后才做加速度为3m/s2的匀加速直线运动，故D错误；故选C．