Question

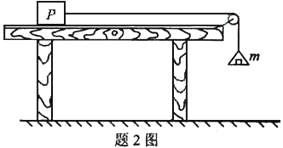
【题目】如图所示，一质量M=2.0kg、长L=0.60m的长木板AB静止在光滑水平面上，木板的左侧固定一半径R=0.60m的四分之一圆弧形轨道，轨道末端的切线水平，轨道与木板靠在一起且末端高度与木板高度相同．现在将质量m=l．0kg的小铁块（可视为质点）从弧形轨道顶端由静止释放，小铁块到达轨道底端时的速度v0=3.0m/s，最终小铁块恰好到达长木板AB最右端．（g=l0m/s2）．求：

（1）小铁块在弧形轨道末端时所受支持力的大小F；

（2）小铁块在弧形轨道上滑动过程中克服摩擦力所做的功Wf；

（3）小铁块和木板AB达到共同速度v及小铁块和木板AB间的动摩擦因数．

Answer 1

【答案】（1）25N；（2）1.5J；（3）1m/s 0.5

【解析】

（1）小木块C做圆周运动，由牛顿第二定律可以求出C受到的支持力；
（2）应用动能定理可以求出小木块在圆弧轨道上滑行时克服摩擦力所做的功；
（3）由动量守恒定律求出速度，然后由能量守恒定律求出动摩擦因数．

（1）小木块通过圆弧形轨道末端时，由牛顿第二定律得：F-mg=m，
解得小木块受到的支持力：F=25N；
（2）小木块在圆弧形轨道上下滑过程中，由动能定理得：mgR-Wf=mv02-0，
解得克服摩擦力做的功Wf=1.5J；
（3）以小铁块与长木板组成的系统为研究对象，以小铁块的初速度方向为正方向，
由动量守恒定律得：mv0=（m+M）v，
由能量守恒定律得：μmgL=mv02-（m+M）v2，
解得：v=1m/s，μ=0.5；