题目内容
有两颗质量均匀分布的行星A和B，它们各有一颗靠近表面的卫星a和b，若这两颗卫星a和b的周期相等，由此可知 ( )．
| A．卫星a和b的线速度大小一定相等 |
| B．行星A和B的质量一定相等 |
| C．行星A和B的密度一定相等 |
| D．行星A和B表面的重力加速度一定相等 |
C
对卫星，由ω＝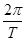
可得，它们的运行角速度一定相等，但它们的轨道半径关系不能确定，故线速度大小不一定相等，A项错；设行星的质量为M，卫星的质量为m，行星的半径为r，由G
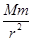＝mr
和M＝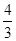
πr3ρ可得，卫星的周期T＝
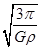，由此公式可得行星A和B的密度一定相同．但由于它们的半径不知，故B、D两项均不能确定．
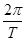可得，它们的运行角速度一定相等，但它们的轨道半径关系不能确定，故线速度大小不一定相等，A项错；设行星的质量为M，卫星的质量为m，行星的半径为r，由G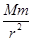＝mr和M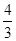＝πr3ρ可得，卫星的周期T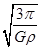＝，由此公式可得行星A和B的密度一定相同．但由于它们的半径不知，故B、D两项均不能确定．
练习册系列答案
相关题目
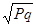
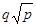
p
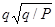
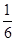，“嫦娥三号”月球探测器的总质量为m,地球表面的重力加速度为g，“环月”运动过程可近似为匀速圆周运动，那么在“环月”运动过程中它的动能可能为（ ）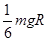
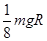
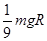
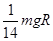
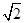∶1
