题目内容
【题目】如图所示,水平地面O点的正上方的装置M每隔相等的时间由静止释放一小球,当某小球离开M的同时,O点右侧一长为L=1.2m的平板车开始以a=6.0m/s2的恒定加速度从静止开始向左运动,该小球恰好落在平板车的左端,已知平板车上表面距离M的竖直高度为h=0.45m.忽略空气的阻力,重力加速度g取10m/s2 . 
(1)求平板车左端离O点的水平距离;
(2)若至少有2个小球落在平板车上,则释放小球的时间间隔△t应满足什么条件?
【答案】
(1)解:设小球自由下落至平板车上表面处历时t0,在该时间段内由运动学方程
对小球有:h= ![]() ①
①
对平板车有:s= ![]() ②
②
由①②式并代入数据可得:s=0.27m.
答:小车左端离O点的水平距离为0.27m;
(2)从释放第一个小球至第2个小球下落到平板车上表面高度处历时△t+t0,设平板车在该时间段内的位移为s1,由运动学方程有:
s1= ![]() ③
③
至少有2个小球落在平板车上须满足:
s1≤s+L ④
由①~④式并代入数据可得:△t≤0.1s.
答:若至少有2个小球落在平板车上,则释放小球的时间间隔△t应满足△t≤0.1s.
【解析】(1)小球自由下落的同时,小车自左向右做匀加速直线运动,根据竖直高度自由落体运动的规律求出运动时间,再根据匀加速运动时间和位移的公式求出水平位移。
(2)先分析从释放第1个小球至第2个小球下落到平板车上表面的时间 关系,然后分析满足至少有2个小球落在平板车上须满足的位移关系,带入可求解。

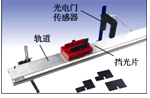
【题目】小明同学在学习了DIS实验后,设计了一个测物体瞬时速度的实验,在小车上固定挡光片,使挡光片的前端与车头齐平,将光电门传感器固定在轨道侧面,垫高轨道的一端.小明同学将小车从该端同一位置由静止释放,获得了如下几组实验数据.则以下表述正确的是( )
实验次数 | 不同的挡光片 | 通过光电门的时间(s) | 速度(m/s) |
第一次 | Ⅰ | 0.23044 | 0.347 |
第二次 | Ⅱ | 0.17464 | 0.344 |
第三次 | Ⅲ | 0.11662 | 0.343 |
第四次 | Ⅳ | 0.05850 | 0.342 |
A.四个挡光片中,挡光片Ⅰ的宽度最小
B.四个挡光片中,挡光片Ⅲ的宽度最小
C.四次实验中,第一次实验测得速度最接近小车车头到达光电门时的瞬时速度
D.四次实验中,第四次实验测得速度最接近小车车头到达光电门时的瞬时速度








