Question

【题目】如图所示，将一劲度系数为k的轻弹簧一端固定在内壁光滑的半球形容器底部O′处(O为球心)，弹簧另一端与质量为m的小球相连，小球静止于P点。已知容器半径为R，与水平面间的动摩擦因数为μ，OP与水平方向的夹角为θ＝30°。下列说法正确的是

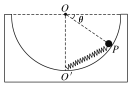
A. 容器相对于水平面有向左运动的趋势

B. 轻弹簧对小球的作用力大小为 mg

C. 容器对小球的作用力竖直向上

D. 弹簧原长为R＋

Answer 1

【答案】BD

【解析】

对容器和小球整体研究，分析受力可求得半球形容器受到的摩擦力．对小球进行受力分析可知，小球受重力、支持力及弹簧的弹力而处于静止，由共点力的平衡条件可求得小球受到的轻弹簧的弹力及小球受到的支持力，由胡克定律求出弹簧的压缩量，即可求得原长．

由于容器和小球组成的系统处于平衡状态，容器相对于水平面没有向左运动的趋势，故A错误；容器对小球的作用力是弹力，指向球心O，故B正确；对小球受力分析，如图所示

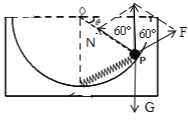
由可知，支持力和弹簧的弹力之间的夹角为120°，则由几何关系可知，小球受到容器的支持力和弹簧对小球的弹力大小均为mg，故C错误；图中弹簧长度为R，压缩量为，故原长为，故D正确。故选BD。