��Ŀ����
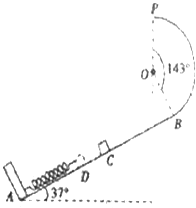
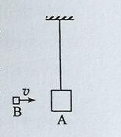
����Ŀ����ͼ����ʾ��ˮƽ���ʹ���˳ʱ�뷽������ת�����ٶ�Ϊv����һС�������ڴ��ʹ�����ˣ�ʹ��Ӿ�ֹ��ʼ�˶������Ӵ��ʹ����A�˶����Ҷ�B������ʱ�����t���ı䴫�ʹ������˶����ٶ�v���ظ������������ɵ�t��vͼ����ͼ����ʾ������ͼ����v��2m/s��ΧΪһˮƽֱ�ߣ�ȡ�������ٶ�g=10m/s2 �� 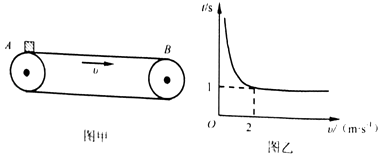
��1��������봫�ʹ���Ķ�Ħ�������̣�
��2�������ʹ������˶����ٶ�v=1m/sʱ��������A�˶�B��ʱ�䣮
���𰸡�
��1���⣺��t��vͼ���֪�������ʹ����ٶ�����2m/s������A�˶���Bʱ�䲻�ٱ仯��˵������ڴ��ʹ���һֱ���ȼ����˶���
���˶���ʽ֪��a= ![]() =
= ![]() =2m/s2��
=2m/s2��
��ţ�ٵڶ�����֪����mg=ma
���=0.2
������봫�ʹ���Ķ�Ħ����������0.2��
��2���⣺�����ʹ����ٶ�����2m/sʱ������ڴ��ʹ���һֱ���ȼ����˶����У�
���ʹ����� L= ![]() =
= ![]() ��1m=1m
��1m=1m
�����ʹ����ٶ�Ϊ1m/sʱ������A�˶���B�����ٵ�1m/s�������˶������ȼ���ʱ��t1��λ��x1�������˶�ʱ��t2��λ��x2
���˶�ѧ��ʽ֪��2ax1=v2
�� x1= ![]() =
= ![]() =0.25m
=0.25m
t1= ![]() =
= ![]() s=0.5s
s=0.5s
���ٹ��̣�t2= ![]() =
= ![]() s=0.75s
s=0.75s
�˶���ʱ�� t=t1+t2=1.25s
�𣺵����ʹ������˶����ٶ�v=1m/sʱ������A�˶�B��ʱ����1.25s��
����������1�������ٶ�ʱ��ͼ������������Լ�ţ�ٵڶ��˶������з��̷�����
��2��ˮƽ���ʹ�������������������ٶȲ��ܳ������ʹ����ٶȡ�������Ŀ�е���Ҫ����������

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�