Question

【题目】如图所示，y轴左侧有方向平行于x轴正方向的匀强电场，电场强度大小E=2.5×105V/m，y轴右侧有垂直纸面向里的匀强磁场，磁感应强度大小B=0.15T，磁场分布在半径R=0.10m的圆形区域内，圆的左端与y轴相切于直角坐标系的原点O，右端与足够长挡板MN相切于x轴上的Q点置于点S的粒子源，可沿x轴正方向射出速度的带正电的粒子流，已知粒子的比荷，SO间距离d=0.10m，粒子重力不计.求：

（1）带电粒子进入磁场时速度的大小；

（2）现以过O点垂直于纸面的直线为轴，将圆形磁场区域按逆时针方向缓慢旋转90°.求：此过程中粒子经过磁场后，打到挡板MN上时，离Q点最远的位置P到Q点的距离L.

Answer 1

【答案】(1) =3.0×106m/s (2) =0.15m. (m、0.15m均给分)

【解析】

(1)S到O，粒子做加速运动，由动能定理：

代入数据得=3.0×106m/s

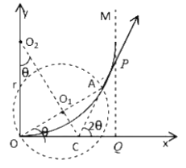
(2)当圆形磁场逆时针旋转到直径OA与x轴方向夹角为时，粒子经过MN上B点时离A最远，如图所示，设粒子做圆周运动的半径为r:

代入数据得r=0.2m，由图知：

所以=30°，P到Q的距离L：

代入数据得：

=0.15m.

答：(1)带电粒子进入磁场时速度的大小=3.0×106m/s；

(2)此过程中粒子经过磁场后，打到挡板MN上时，离Q点最远的位置P到Q点的距离L=0.15m.