题目内容
20.如图甲,倾角为θ的光滑斜面上放一轻质弹簧,其下端固定,静止时上端位置在B点,在A点放一质量m=2kg的小物块,小物块自由释放,在开始运动的一段时间内v-t图如图乙所示,小物块在0.4s时运动到B点,在0.9s时到达C点,BC的距离为1.2m(g取10m/s2).由图知( )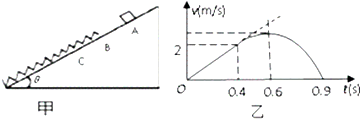
| A. | 斜面倾角θ=$\frac{π}{6}$ | |
| B. | C点处弹簧的弹性势能为16J | |
| C. | 物块从B运动到C的过程中机械能守恒 | |
| D. | 物块从C回到A的过程中,加速度先减小后增大,再保持不变 |
分析 由图象求出物块的加速度,然后由牛顿第二定律求出斜面的倾角;由能量守恒定律求出弹簧的弹性势能;根据机械能守恒的条件判断机械能是否守恒;根据物块的受力情况应用牛顿第二定律判断物块加速度如何变化.
解答 解:A、由图乙所示图象可知,在0-4s内,物块做匀加速直线运动,加速度为:a=$\frac{△v}{△t}$=$\frac{2}{0.4}$=5m/s2,由牛顿第二定律得:mgsinθ=ma,
解得:sinθ=$\frac{a}{g}$=0.5,则θ=$\frac{π}{6}$,故A正确;
B、由能量守恒定律可得,在C点弹簧的弹性势能为:
EP=$\frac{1}{2}$mvB2+mghBC=$\frac{1}{2}$×2×22+2×10×1.2×sin$\frac{π}{6}$=16J,故B正确.
C、物体从B到C过程,除重力做功外,弹簧弹力对物块做负功,物块的机械能不守恒,故C错误.
D、物块从C点回到A点过程中,开始弹簧的弹力大于重力沿斜面向下的分力,合力向上,物块向上做加速运动,弹力逐渐减小,物块所受合力减小,物块的加速度减小,然后弹簧的弹力小于重力沿斜面向下的分力,合力向下,物块做减速运动,随物块向上运动,弹簧弹力变小,物块受到的合力变大,加速度变大,当物体与弹簧分离后,物块受到的合力等于重力的分力,加速度不变,物块做加速度不变的减速运动,由此可知在整个过程中,物块的加速度先减小后增大,再保持不变,故D正确;
故选:ABD
点评 本题考查了求斜面的倾角、判断物体机械能是否守恒、求弹簧的弹性势能、判断物块加速度如何变化等问题,分析清楚物块运动过程、由图乙所示图象求出物块的速度、应用牛顿第二定律、能量守恒定律即可正确解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.如图所示为某质点的速度-时间图象,则下列说法中正确的是( )


| A. | 在0~6s内,质点做匀变速直线运动 | B. | 在t=12s末,质点的加速度为-1m/s2 | ||
| C. | 在6~10s内,质点处于静止状态 | D. | 在4s末,质点运动方向改变 |
9.作用在同一点的两个力,大小分别为5N和2N,则它们的合力不可能是( )
| A. | 5N | B. | 4N | C. | 2N | D. | 9N |
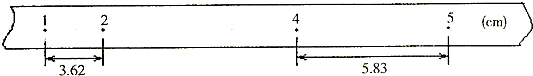
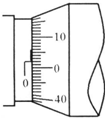 在“测定金属的电阻率”的实验中,用螺旋测微器测量金属丝直径时的刻度位置如图所示,用米尺测量金属丝的长度l=0.810m.金属丝的电阻大约为4Ω.先用伏安法测出金属丝的电阻,然后根据电阻定律计算出该金属材料的电阻率.
在“测定金属的电阻率”的实验中,用螺旋测微器测量金属丝直径时的刻度位置如图所示,用米尺测量金属丝的长度l=0.810m.金属丝的电阻大约为4Ω.先用伏安法测出金属丝的电阻,然后根据电阻定律计算出该金属材料的电阻率.