题目内容
如右图所示,在方向竖直向下的匀强电场中,一个质量为m、带负电的小球从斜直轨道上的A点由静止滑下,小球通过半径为R的圆轨道顶端的B点时恰好不落下来.若轨道是光滑绝缘的,小球的重力是它所受的电场力2倍,试求: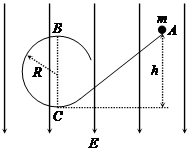
⑴A点在斜轨道上的高度h;
⑵小球运动到最低点C时,圆轨道对小球的支持力.
(1)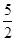 R (2) 3mg
R (2) 3mg
解析试题分析:由题意得:mg=2Eq
设小球到B点的最小速度为VB,则由牛顿第二定律可得:
mg-Eq=m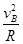 ;
;
对AB过程由动能定理可得:
mg(h-2R)-Eq(h-2R)=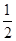 mVB2;
mVB2;
联立解得:h=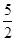 R;
R;
(2)对AC过程由动能定理可得:
mgh-Eqh=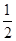 mvc2;
mvc2;
由牛顿第二定律可得:
F+Eq-mg=m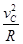
联立解得:F=3mg;由牛顿第三定律可得小球对轨道最低点的压力为3mg.
考点:牛顿定律及动能定理。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
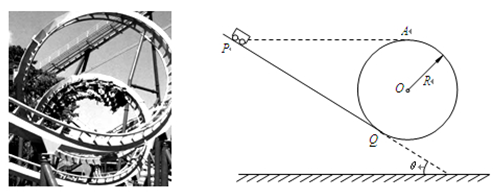
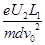 。工件质量M=0.8Kg,与地面间的动摩擦因数
。工件质量M=0.8Kg,与地面间的动摩擦因数 。(取g=10m/s2)
。(取g=10m/s2)
 时,使工件立刻停止运动(即不考虑减速的时间和位移),物块飞离圆弧轨道落至BC段,求物块的落点与B点间的距离。
时,使工件立刻停止运动(即不考虑减速的时间和位移),物块飞离圆弧轨道落至BC段,求物块的落点与B点间的距离。 =1.0×108 C/kg,粒子的重力和粒子间的相互作用都忽略不计,在粒子通过电场区域的极短时间内极板间的电压可以看作不变.求:
=1.0×108 C/kg,粒子的重力和粒子间的相互作用都忽略不计,在粒子通过电场区域的极短时间内极板间的电压可以看作不变.求:

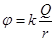 ,其中k为静电力常量,设无穷远处电势为零)。
,其中k为静电力常量,设无穷远处电势为零)。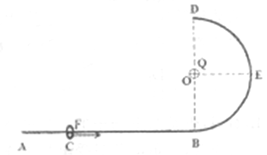
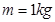 的滑块,在水平力作用下静止在倾角为
的滑块,在水平力作用下静止在倾角为 的光滑斜面上,斜面的末端B与水平传送带相接(物块经过此位置滑上皮带时无能量损失),传送带的运行速度为
的光滑斜面上,斜面的末端B与水平传送带相接(物块经过此位置滑上皮带时无能量损失),传送带的运行速度为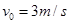 ,长为
,长为 。今将水平力撤去,当滑块滑到传送带右端C时,恰好与传送带速度相同。已知滑块与传送带间的动摩擦因数为
。今将水平力撤去,当滑块滑到传送带右端C时,恰好与传送带速度相同。已知滑块与传送带间的动摩擦因数为 (
( )。求:
)。求:
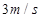 ,则滑块在传送带上滑行的整个过程中产生的热量为多少.
,则滑块在传送带上滑行的整个过程中产生的热量为多少.
 ,那么物块能否紧贴圆环在竖直平面内做圆周运动。(写出详细分析、判定过程)(已知:
,那么物块能否紧贴圆环在竖直平面内做圆周运动。(写出详细分析、判定过程)(已知: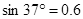 ;
;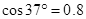 )
)