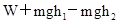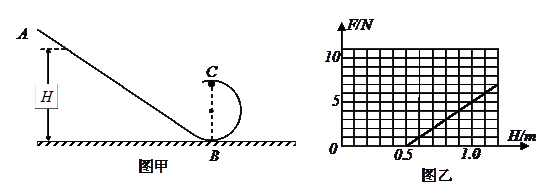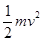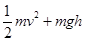题目内容
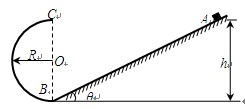
如图所示,一光滑的半圆形轨道处于竖直平面内,并和一粗糙的斜面相接,其半径大小为R=0.4m,直径BC在竖直方向上,一小物体放在斜面上的A点,离水平面高度为h=3m,小物体与斜面之间的动摩擦因数为μ=0.5,斜面倾角θ=37o。已知sin37o=0.6,cos37o=0.8,重力加速度g=10m/s2,现在把小物体从静止开始自由释放,求:
(1)小物体运动到斜面底端B点时速度的大小?
(2)证明小物体可以沿半圆形轨道运动到最高点C;
(3)小物体离开半圆轨道后第一次落到斜面上时,其速度v的大小。

(1)小物体运动到斜面底端B点时速度的大小?
(2)证明小物体可以沿半圆形轨道运动到最高点C;
(3)小物体离开半圆轨道后第一次落到斜面上时,其速度v的大小。
(1)4.5m/s(2)2m/s(3)3.2m/s
试题分析:(1)根据动能定理:
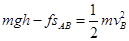 ①
①又:
 ②
② ③
③解得:
 ④
④(2)小物体在C点,有:
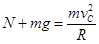 ⑤
⑤当N=0时,Vc有最小值,可得:
 ⑥
⑥从B到C,由机械能守恒,可得:
 ⑦
⑦解得:Vc=2(m/s) ⑧
(3)设落到斜面时水平位移为S,下落高度为h,由动能定理:
 ⑨
⑨又:
 ⑩
⑩ ⑾
⑾联立可得:
 ⑿
⑿点评:在使用动能定理解决多过程问题时,可给我们解题带来很大的方便,但是关键需要判断清楚各个过程中力的做功情况以及过程的始末状态

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
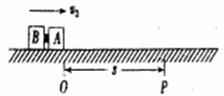
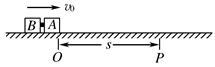
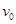 一起从O点滑出,滑行一段距离后到达P点,速度变为
一起从O点滑出,滑行一段距离后到达P点,速度变为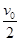 ,此时炸药爆炸使木块A、B脱离,发现木块B立即停在原位置,木块A继续沿水平方向前进.已知O、P两点间的距离为s,炸药爆炸时释放的化学能均全部转化为木块的动能,爆炸时间很短可以忽略不计.求:
,此时炸药爆炸使木块A、B脱离,发现木块B立即停在原位置,木块A继续沿水平方向前进.已知O、P两点间的距离为s,炸药爆炸时释放的化学能均全部转化为木块的动能,爆炸时间很短可以忽略不计.求: