题目内容
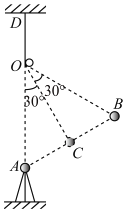
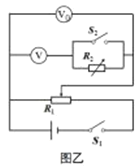
【题目】如图所示，半径为R的3/4光滑绝缘圆形轨道固定在竖直面内,以圆形轨道的圆心O为坐标原点，沿水平直径方向建立X轴，竖直方向建立Y轴．Y轴右侧存在竖直向下范围足够大的匀强电场，电场强度大小为
，第二象限存在匀强电场E2 (方向与大小均未知)．不带电的绝缘小球a质量为M，带电量为+q的小球b质量为m ,a球从与圆心等高的轨道A处由静止开始沿轨道下滑，与静止于轨道最低点的b球正碰，碰撞后b球恰好能通过轨道最高点C，并落回轨道A处，小球落回A处时的速度大小与小球离开最高点C时速度大小相等，重力加速度为g，小球b的电量始终保持不变．试求：
(1) 第一次碰撞结束后，小球a的速度大小；
(2) 第二象限中电场强度E2的大小和方向；
(3) 小球b从B点运动到A点的过程中电势能的变化量．
【答案】（1）
；（2）E2= 
，方向水平向右；（3）
【解析】
（1）根据机械能守恒定律可求a球到B点的速度，根据动能定理和牛顿第二定律可求b球在B点速度，根据动量守恒定律可求碰撞后a的速度大小；
（2）根据C、A速度大小相等，可知此过程合力垂直CA连线，分别沿CA方向和垂直CA方向列运动方程，根据牛顿第二定律和电场力公式可求电场强度；
（3）对小球b从B到A过程中，根据能量守恒定律或功能关系可求电势能的变化量．
(1)设小球a滑动到最低时速度为
由机械能守恒得：
.......................①
设a、b小球在B点碰撞后的速度分别为
，b球过最高点速度为
有：
.............................②
.................③
...................................
④
把数据代入①②③④式，解得 ：
（2）要让b小球落回A处时的速度大小与小球离开最高点C时速度大小相等，电场力E2q与mg的合力应垂直于AC边斜向下
把运动沿CA方向与垂直CA方向分解，CA方向做匀速直线运动，垂直CA方向做匀减速运动
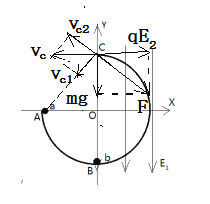
如图：
.............⑤
.............⑥
由几何关系得：CA长
.............⑦
设小球b从C运动到A点时间为t ，小球b垂直CA方向加速度大小为a
有：
..................................⑧
.............⑨
解得：
，小球从C到A受到的合力
由几何关系电场力大小为F电=mg，方向水平向右
根据F电=E2q，E2= ，方向水平向右；
(3)法一：小球b从B到A过程中，电场力做功：
电势能变化量
法二：由能量守恒定律得：
