题目内容
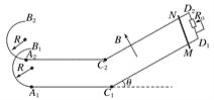
【题目】如图所示,倾角为θ、宽度为d、长为L的光滑倾斜导轨C1D1、C2D2顶端接有可变电阻R0,L足够长,倾斜导轨置于垂直导轨平面斜向左上方的匀强磁场中,磁感应强度为B,C1A1B1、C2A2B2为绝缘轨道,由半径为R处于竖直平面内的光滑半圆环A1B1、A2B2和粗糙的水平轨道C1A1、C2A2组成,粗糙的水平轨道长为s,整个轨道对称.在导轨顶端垂直于导轨放一根质量为m、电阻不计的金属棒MN,使其从静止开始自由下滑,不考虑金属棒MN经过接点A、C处时机械能的损失,整个运动过程中金属棒始终保持水平,水平导轨与金属棒MN之间的动摩擦因数μ.则:
(1)金属棒MN在倾斜导轨CD上运动的过程中,电阻R0上产生的热量Q为多少?
(2)为了金属棒MN能到达光滑半圆环B点,可变电阻R0应满足什么条件?
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:金属棒下滑时切割磁感线运动,产生感应电动势,产生感应电流,受到沿斜面向上的安培力,做加速度逐渐减小的加速运动,当加速度为0时,速度最大.下滑过程中,重力势能减小,动能增加,内能增加,根据能量守恒求出整个电路产生的热量,从而求出电阻R上产生的热量.对金属棒到达最高点进行受力分析,确定能到达最高点的最小速度,再由动能定理从而来计算出可变电阻R0应满足条件。
(1)由于L足够长,棒MN在斜导轨上到达C端前已经做匀速运动
棒受到的安培力: ![]()
根据平衡条件可得: ![]()
解得: ![]()
根据能量守恒: ![]()
所以![]()
(2)棒能到达B点时: ![]()
可得: ![]()
从C点到B点的过程![]()
可得: ![]()

练习册系列答案
相关题目