题目内容
12.物体从A到D由静止开始做匀加速直线运动,B、C把AD分成相等的三段,(1)则物体分别通过这三段位移的时间之比是1:($\sqrt{2}$-1):($\sqrt{3}$-$\sqrt{2}$);
(2)物体在这段位移的平均速度之比是1:($\sqrt{2}$+1):($\sqrt{3}$+$\sqrt{2}$);
(3)物体在B、C、D三点速度之比是1:$\sqrt{2}$:$\sqrt{3}$.
分析 根据位移公式可求得物体在AB、AC及AD段的时间,则可求得通过AB、BC及CD段的时间;再由平均速度公式可求得平均速度;根据速度公式可求得物体在BCD三点的速度.
解答 解:(1)设AB=BC=CD=x;
由位移公式可得:
AB段有:x=$\frac{1}{2}$at12
AC段有:2x=$\frac{1}{2}$at22
AD段有3x=$\frac{1}{2}$at32
则可知通过AB的时间t1=$\sqrt{\frac{2x}{a}}$
BC段的时间tII=t2-t1=$\sqrt{\frac{4x}{a}}$-$\sqrt{\frac{2x}{a}}$
CD段的时间tIII=t3-t2=$\sqrt{\frac{6x}{a}}$-$\sqrt{\frac{4x}{a}}$
故三段位移内的时间之比为:tI:tII:tIII=1:($\sqrt{2}$-1):($\sqrt{3}$-$\sqrt{2}$)
(2)平均速度等于位移与时间的比值,则可知:
平均速度之比为:$\overline{{v}_{AB}}$:$\overline{{v}_{BC}}$:$\overline{{v}_{CD}}$=1:$\frac{1}{\sqrt{2}-1}$:$\frac{1}{\sqrt{3}-\sqrt{2}}$=1:($\sqrt{2}$+1):($\sqrt{3}$+$\sqrt{2}$)
(3)由速度公式可得:v=at,则BCD三点的速度之比为:
vB:vC:vD=t1:t2:t3=1:$\sqrt{2}$:$\sqrt{3}$
故答案为:(1)1:($\sqrt{2}$-1):($\sqrt{3}$-$\sqrt{2}$);(2)1:($\sqrt{2}$+1):($\sqrt{3}$+$\sqrt{2}$);(3)1:$\sqrt{2}$:$\sqrt{3}$
点评 本题考查初速度为零的匀变速直线运动的规律推导,要注意明确三段为相邻相等的位移,且初速度为零,故从起点开始列式最为简单.

| A. | 它可以定位在北京正上方太空 | |
| B. | 它的轨道平面一定与赤道平面重合 | |
| C. | 若要发射一颗质量为2.4t的地球同步卫星,则该卫星的轨道半径将比“亚洲一号”卫星的轨道半径小 | |
| D. | 若发射质量为2.4t的地球同步卫星,则该卫星的轨道半径将比“亚洲一号”卫星的轨道半径大 |
| A. | 4 m | B. | 36 m | C. | 6.25 m | D. | 以上答案都不对 |
| A. | -3.0×1O4 V | B. | 3.0×104 V | C. | -7.0×104 V | D. | 7.0×104 V |
| A. | 等于$\frac{x}{t}$ | B. | 等于$\frac{2x}{t}$ | C. | 大于$\frac{2x}{t}$ | D. | 小于$\frac{2x}{t}$ |

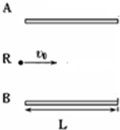 如图所示,两平行金属板A、B,两极板长L=8cm,两极板间距离d=8cm,极板间匀强电场的电场强度大小E=3750N/C,方向竖直向下,一带正电的粒子电荷量q=10-10C,质量m=10-20kg,从R点沿电场中心线垂直电场线飞入电场,初速度v0=2×106m/s,不考虑重力影响,求:
如图所示,两平行金属板A、B,两极板长L=8cm,两极板间距离d=8cm,极板间匀强电场的电场强度大小E=3750N/C,方向竖直向下,一带正电的粒子电荷量q=10-10C,质量m=10-20kg,从R点沿电场中心线垂直电场线飞入电场,初速度v0=2×106m/s,不考虑重力影响,求: