题目内容
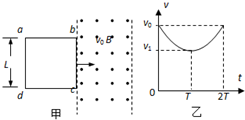 (2008?泰州模拟)如图甲所示,光滑绝缘水平面上一矩形金属线圈abcd的质量为m、电阻为R、ad边长度为L,其右侧是有左右边界的匀强磁场,磁场方向垂直纸面向外,磁感应强度大小为B,ab边长度与有界磁场区域宽度相等,在t=0时刻线圈以初速度v0进入磁场,在t=T时刻线圈刚好全部进入磁场且速度为v1,此时对线圈施加一沿运动方向的变力F,使线圈在t=2T时刻线圈全部离开该磁场区,若上述过程中线圈的v-t图象如图乙所示,整个图象关于t=T轴对称.
(2008?泰州模拟)如图甲所示,光滑绝缘水平面上一矩形金属线圈abcd的质量为m、电阻为R、ad边长度为L,其右侧是有左右边界的匀强磁场,磁场方向垂直纸面向外,磁感应强度大小为B,ab边长度与有界磁场区域宽度相等,在t=0时刻线圈以初速度v0进入磁场,在t=T时刻线圈刚好全部进入磁场且速度为v1,此时对线圈施加一沿运动方向的变力F,使线圈在t=2T时刻线圈全部离开该磁场区,若上述过程中线圈的v-t图象如图乙所示,整个图象关于t=T轴对称.(1)求t=0时刻线圈的电功率;
(2)线圈进入磁场的过程中产生的焦耳热和穿过磁场过程中外力F所做的功分别为多少?
(3)若线圈的面积为S,请运用牛顿第二运动定律和电磁学规律证明:在线圈进人磁场过程中v0-v1=
| B2LS | mR |
分析:(1)t=0时,母亲线圈产生的感应电动势E=BLv0,电功率P=
.
(2)线圈进入磁场的过程中动能转化为焦耳热,由能量守恒求焦耳热.外力做功一是增加动能,二是克服安培力做功,由功能关系求得外力做功.
(3)运用微元法思想,将时间分为若干等分,每一等分可看成匀变速运动,由公式△v=at列式,得到速度的变化量与电流的关系,由电量公式公式Q=It,得到速度的变化量与感应电荷量的关系,再根据法拉第定律、欧姆定律得到感应电荷量Q=
=
,联立即可得到证明.
| E2 |
| R |
(2)线圈进入磁场的过程中动能转化为焦耳热,由能量守恒求焦耳热.外力做功一是增加动能,二是克服安培力做功,由功能关系求得外力做功.
(3)运用微元法思想,将时间分为若干等分,每一等分可看成匀变速运动,由公式△v=at列式,得到速度的变化量与电流的关系,由电量公式公式Q=It,得到速度的变化量与感应电荷量的关系,再根据法拉第定律、欧姆定律得到感应电荷量Q=
| △φ |
| R |
| BS |
| R |
解答:解:(1)t=0时,E=BLv0
线圈电功率P=
=
(2)线圈进入磁场的过程中动能转化为焦耳热
Q=
mv02-
mv12
外力做功一是增加动能,二是克服安培力做功
WF=△Ek+Q=mv02-mv12
(3)根据微元法思想,将时间分为若干等分,每一等分可看成匀变速
vn-vn+1=
tn
∴v0-v1=
(I1t1+I2t2+…+Intn)
其中I1t1+I2t2+…+Intn=Q
电量Q=It=
=
∴v0-v1=
答:
(1)t=0时刻线圈的电功率是
;
(2)线圈进入磁场的过程中产生的焦耳热和穿过磁场过程中外力F所做的功分别为
mv02-
mv12和mv02-mv12.
(3)证明略.
线圈电功率P=
| E2 |
| R |
| B2L2v02 |
| R |
(2)线圈进入磁场的过程中动能转化为焦耳热
Q=
| 1 |
| 2 |
| 1 |
| 2 |
外力做功一是增加动能,二是克服安培力做功
WF=△Ek+Q=mv02-mv12
(3)根据微元法思想,将时间分为若干等分,每一等分可看成匀变速
vn-vn+1=
| BLIn |
| m |
∴v0-v1=
| BL |
| m |
其中I1t1+I2t2+…+Intn=Q
电量Q=It=
| △φ |
| R |
| BS |
| R |
∴v0-v1=
| B2LS |
| mR |
答:
(1)t=0时刻线圈的电功率是
| B2L2v02 |
| R |
(2)线圈进入磁场的过程中产生的焦耳热和穿过磁场过程中外力F所做的功分别为
| 1 |
| 2 |
| 1 |
| 2 |
(3)证明略.
点评:解决本题的关键能够熟练运用能量守恒定律,知道线圈进磁场的过程和出磁场过程产生的热量相等.并能运用微元法处理非匀变速运动的问题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 (2008?泰州模拟)如图所示,两种不同的正离子(不计重力)垂直射人偏转电场,从偏转电场射出时具有相同的偏转距离y和偏转角θ(偏转电压U保持不变),则两种离子进入偏转电场前只要满足( )
(2008?泰州模拟)如图所示,两种不同的正离子(不计重力)垂直射人偏转电场,从偏转电场射出时具有相同的偏转距离y和偏转角θ(偏转电压U保持不变),则两种离子进入偏转电场前只要满足( ) (2008?泰州模拟)我国计划在2025年实现载人登月,并在绕月轨道上建造 空间站.如图所示,关闭动力的航天飞机在月球引力作用下向月球靠近,并将与空间站在B处对接,已知空间站绕月轨道半径为r,周期为T,万有引力常量为G,下列说法中正确的是( )
(2008?泰州模拟)我国计划在2025年实现载人登月,并在绕月轨道上建造 空间站.如图所示,关闭动力的航天飞机在月球引力作用下向月球靠近,并将与空间站在B处对接,已知空间站绕月轨道半径为r,周期为T,万有引力常量为G,下列说法中正确的是( )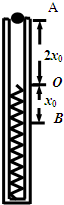 (2008?泰州模拟)如图所示,在一直立的光滑管内放置一轻质弹簧,上端O点与管口A的距离为2X0,一质量为m的小球从管口由静止下落,将弹簧压缩至最低点B,压缩量为x0,不计空气阻力,则( )
(2008?泰州模拟)如图所示,在一直立的光滑管内放置一轻质弹簧,上端O点与管口A的距离为2X0,一质量为m的小球从管口由静止下落,将弹簧压缩至最低点B,压缩量为x0,不计空气阻力,则( ) (2008?泰州模拟)如图所示,电流表A1(0~3A)和A2(0~0.6A)是由两个相同的电流表改装而成,现将这两个电流表并联后接入电路中,闭合开关S,调节滑动变阻器,下列说法中正确的是( )
(2008?泰州模拟)如图所示,电流表A1(0~3A)和A2(0~0.6A)是由两个相同的电流表改装而成,现将这两个电流表并联后接入电路中,闭合开关S,调节滑动变阻器,下列说法中正确的是( )