Question

【题目】如图所示，在竖直平面内有一直角坐标系O-xy，在该平面内有一平行y轴的匀强电场，大小为E，方向竖直向下。一过坐标原点与x轴成θ = 60°角的无穷大的平板与竖直平面垂直。在y轴上某点有一质量为m。电荷量为+q的粒子以某一速度垂直电场射入电场，经过时间t1时，在该平面内再另加一匀强电场E1，粒子再经过时间t2且t1= t2= t时，恰好垂直接触平板，且接触平板时速度为零，忽略粒子所受的重力，求：

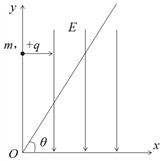
(1)粒子射入电场时的速度大小和在y轴上的位置；

(2)E1的大小以及与y轴之间的夹角α的正切值。

Answer 1

【答案】（1） （2），。

【解析】(1)设粒子的初速度为v0，在t1时间内做类平抛运动，粒子在电场中的加速度为

粒子在电场中的竖直速度为，按题意分析得到：

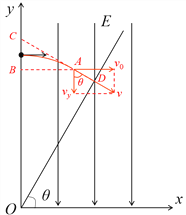
联立解得粒子抛出时速度

t1时刻粒子的速度为

对应的位移为：

加电场E1后，粒子从A到D做匀减速直线运动，故有：

又

所以

故抛出点的y坐标为。

(2)如图所示，设E1方向与y轴成α角，由粒子从A到D的匀减速直线运动有：

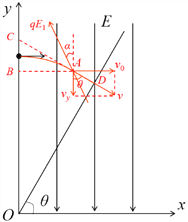
联立解得：，。