Question

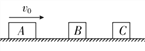
【题目】光滑水平轨道上有三个木块A、B、C，质量分别为、，开始时B、C均静止，A以初速度向右运动，A与B碰撞后分开，B又与C发生碰撞并粘在一起，此后A与B间的距离保持不变。求:

(1)B与C碰撞前，B的速度大小；

(2)整个过程中物体A所受合外力冲量的大小。

Answer 1

【答案】(1) (2)

【解析】【试题分析】由于水平轨道光滑，碰撞过程符合动量守恒的条件：合外力为零，此题要分两步求解：第一步：由动量守恒定律求出A与B碰撞的过程列式．第二步根据动量守恒定律对B与C碰撞过程列式，抓住最终A与B的速度相同，联立即可求解．

(1)设A与B碰撞后，A的速度为vA，B与C碰撞前B的速度为vB，B与C碰撞后粘在一起的速度为v，取向右为正方向．

由动量守恒定律得：A、B木块碰撞过程有：3mv0=3mvA+mvB ①

B、C木块碰撞过程有：mvB=(m+m)v ②

由A与B间的距离保持不变得 :vA=v ③

联立①②③式，代入数据得 , ④

(2)对于A，由动量定理得 ⑤

联立得 ，方向水平向左 ⑥

则冲量的大小为