题目内容
3.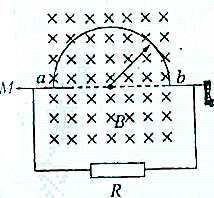 将硬导线中间一段折为半圆形是,使其半径为r(m),让它在磁感应强度为B(T)、方向如图所示的匀强磁场中绕轴MN匀速转动,转速为n(r/s),导线在a、b两处通过电刷与外电路连接,外电路接有阻值为R(Ω)的电阻,其余部分的电阻不计,则( )
将硬导线中间一段折为半圆形是,使其半径为r(m),让它在磁感应强度为B(T)、方向如图所示的匀强磁场中绕轴MN匀速转动,转速为n(r/s),导线在a、b两处通过电刷与外电路连接,外电路接有阻值为R(Ω)的电阻,其余部分的电阻不计,则( )| A. | 通过电阻R的电流恒为$\frac{Bn{π}^{2}{r}^{2}}{R}$ | |
| B. | 电阻R两端的电压的最大值为Bnπ2r2 | |
| C. | 半圆导线从图示位置转过180°的过程中,通过电阻R的电荷量为$\frac{Bπ{r}^{2}}{R}$ | |
| D. | 电阻R上消耗的电功率为$\frac{(Bb{π}^{2}{r}^{2})^{2}}{2R}$ |
分析 线框转动过程产生正弦式交流电,求出感应电动势的最大值,然后应用欧姆定律求出电压最大值,应用法拉第电磁感应定律求出感应电动势,由欧姆定律与电流定义式求出电荷量;应用电功率公式求出电阻消耗的电功率.
解答 解:A、线圈匀速转动过程,线圈产生正弦式交变电流,通过电阻R的电流按正弦规律变化,故A错误;
B、感应电动势的最大值:Em=BSω=B×$\frac{1}{2}$πr2×2πn=nπ2r2B,除R外,其余电阻不计,则电阻R两端电压的最大值:U=Em=nπ2r2B,故B正确;
C、由法拉第电磁感应定律可知,半圆导线从图示位置转过180°的过程中平均感应电动势:E=$\frac{△Φ}{△t}$=$\frac{2BS}{△t}$=$\frac{2B×\frac{1}{2}π{r}^{2}}{△t}$=$\frac{πB{r}^{2}}{△t}$,感应电流:I=$\frac{E}{R}$,通过R的电荷量:q=I△t,解得:q=$\frac{πB{r}^{2}}{R}$,故C正确;
D、电动势的有效值:E有效=$\frac{{E}_{m}}{\sqrt{2}}$=$\frac{n{π}^{2}{r}^{2}B}{\sqrt{2}}$,电阻R上消耗的电功率:P=$\frac{({E}_{有效})^{2}}{R}$=$\frac{(n{π}^{2}{r}^{2}B)^{2}}{2R}$,故D正确;
故选:BCD.
点评 线圈转动过程产生正弦式交变电流,求出感应电动势的最大值、应用法拉第电磁感应定律、欧姆定律、电流定义式、掌握最大值与有效值间的关系、应用电功率公式空可以解题;此外感应电量q=n$\frac{△Φ}{R}$是常用的经验公式,要理解并加强记忆.

练习册系列答案
相关题目
13.物体做平抛运动时,在任意相同时间间隔内,速度的变化量( )
| A. | 大小不同,方向不同 | B. | 大小相同,方向不同 | ||
| C. | 大小不同,方向相同 | D. | 大小相同,方向相同 |
15.X射线( )
| A. | 不是电磁波 | B. | 具有反射和折射的特性 | ||
| C. | 只能在介质中传播 | D. | 不能发生干涉和衍射 |
12.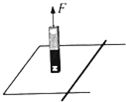 如图,光滑平行金属导轨固定在水平面上,左端由导线相连,导体棒垂直静置于导轨上构成回路.在外力F作用下,回路上方的条形磁铁竖直向上做匀速运动.在匀速运动过程中外力F做功WF,磁场力对导体棒做功W1,磁铁克服磁场力做功W2,重力对磁铁做功WG,回路中产生的焦耳热为Q,导体棒获得的动能为EK.则( )
如图,光滑平行金属导轨固定在水平面上,左端由导线相连,导体棒垂直静置于导轨上构成回路.在外力F作用下,回路上方的条形磁铁竖直向上做匀速运动.在匀速运动过程中外力F做功WF,磁场力对导体棒做功W1,磁铁克服磁场力做功W2,重力对磁铁做功WG,回路中产生的焦耳热为Q,导体棒获得的动能为EK.则( )
 如图,光滑平行金属导轨固定在水平面上,左端由导线相连,导体棒垂直静置于导轨上构成回路.在外力F作用下,回路上方的条形磁铁竖直向上做匀速运动.在匀速运动过程中外力F做功WF,磁场力对导体棒做功W1,磁铁克服磁场力做功W2,重力对磁铁做功WG,回路中产生的焦耳热为Q,导体棒获得的动能为EK.则( )
如图,光滑平行金属导轨固定在水平面上,左端由导线相连,导体棒垂直静置于导轨上构成回路.在外力F作用下,回路上方的条形磁铁竖直向上做匀速运动.在匀速运动过程中外力F做功WF,磁场力对导体棒做功W1,磁铁克服磁场力做功W2,重力对磁铁做功WG,回路中产生的焦耳热为Q,导体棒获得的动能为EK.则( )| A. | W1=Q | B. | W2-W1=Q | C. | W1=EK | D. | WF+WG=Q+EK |
10. 表为如图所示“风光互补路灯”中风力发电机部分的配置参数.已知风轮机叶片旋转所扫过的面积为风力发电机可接受风能的面积,风力发电机的输出功率与单位时间内流向风轮机的最大风能P风成正比.则当风垂直通过叶片旋转扫过的平面且风速为6m/s时(忽略空气密度的变化),风力发电机的输出功率为( )
表为如图所示“风光互补路灯”中风力发电机部分的配置参数.已知风轮机叶片旋转所扫过的面积为风力发电机可接受风能的面积,风力发电机的输出功率与单位时间内流向风轮机的最大风能P风成正比.则当风垂直通过叶片旋转扫过的平面且风速为6m/s时(忽略空气密度的变化),风力发电机的输出功率为( )
 表为如图所示“风光互补路灯”中风力发电机部分的配置参数.已知风轮机叶片旋转所扫过的面积为风力发电机可接受风能的面积,风力发电机的输出功率与单位时间内流向风轮机的最大风能P风成正比.则当风垂直通过叶片旋转扫过的平面且风速为6m/s时(忽略空气密度的变化),风力发电机的输出功率为( )
表为如图所示“风光互补路灯”中风力发电机部分的配置参数.已知风轮机叶片旋转所扫过的面积为风力发电机可接受风能的面积,风力发电机的输出功率与单位时间内流向风轮机的最大风能P风成正比.则当风垂直通过叶片旋转扫过的平面且风速为6m/s时(忽略空气密度的变化),风力发电机的输出功率为( )| 最小启动风速 | 1.0m/s |
| 最小充电风速 | 2.0m/s |
| 最大限制风速 | 12.0m/s |
| 最大输出功率 | 400W |
| A. | 25 W | B. | 50 W | C. | 100 W | D. | 200 W |
 如图电容器AB,电容器UAB=+U,两极板的距离为d,质量为m的小球,电量为-q.从静止从B板运动A板.
如图电容器AB,电容器UAB=+U,两极板的距离为d,质量为m的小球,电量为-q.从静止从B板运动A板.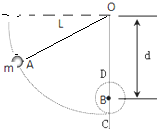 质量为m的小球A用不可伸长的细绳悬于O点,在O点的正下方有一固定的钉子B,OB=d,初始时绳子拉直,且与水平方形呈30°夹角,将小球A无初速度释放,绳长为L,如图所示,试求:
质量为m的小球A用不可伸长的细绳悬于O点,在O点的正下方有一固定的钉子B,OB=d,初始时绳子拉直,且与水平方形呈30°夹角,将小球A无初速度释放,绳长为L,如图所示,试求: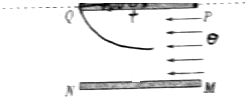 MN、PQ是长为d,间距为d的两块平行金属板,PQ板带正电,MN板带负电,在PQ板所处水平线上方足够大空间内有垂直纸面的匀强磁场,如图所示,一束粒子以相同的速度v0平行两极板射入电场,其中沿两板中线射入的粒子恰好能从PQ板左边缘射入磁场,然后又恰好从PQ板的右边缘射出磁场,已知粒子电荷量为q、质量为m,不计粒子重力、忽略电场的边缘效应,磁感应强度大小B=$\frac{2m{v}_{0}}{qd}$.
MN、PQ是长为d,间距为d的两块平行金属板,PQ板带正电,MN板带负电,在PQ板所处水平线上方足够大空间内有垂直纸面的匀强磁场,如图所示,一束粒子以相同的速度v0平行两极板射入电场,其中沿两板中线射入的粒子恰好能从PQ板左边缘射入磁场,然后又恰好从PQ板的右边缘射出磁场,已知粒子电荷量为q、质量为m,不计粒子重力、忽略电场的边缘效应,磁感应强度大小B=$\frac{2m{v}_{0}}{qd}$.